
В соответствии с классической теорией электронной проводимости удельное сопротивление металлов должно уменьшаться при понижении температуры, но при всех температурах являться конечным. Подобная зависимость сопротивления наблюдается в эксперименте при относительно высоких температурах. Если температура будет всего несколько кельвинов, то зависимость сопротивления от температуры качественно изменится. Прежде всего, удельное сопротивление становится независимым от температуры и стремится к некоторому определенному значению. Это значение отлично для разных веществ и даже разных образцов одного вещества. Экспериментально установлено, что остаточное сопротивление тем меньше, чем чище металл и чем меньше структурных дефектов в образце.
Если понижать температуру еще больше, то в некоторых веществах наблюдается явление сверхпроводимости. Это явление открыто Камерлинг -- Онессом в 1911 г. При некоторой определенной температуре, свойственной каждому веществу, удельное сопротивление скачком уменьшается почти до нуля. Температуры перехода в сверхпроводящее состояние всегда очень низкие.
Сверхпроводимость среди чистых веществ имеют алюминий, кадмий, цинк, индий, галлий. Свойство сверхпроводимости связано со структурой кристаллической решетки.
Сверхпроводимость может наблюдаться не только у чистых веществ, но и в некоторых соединениях и сплавах, причем сами элементы, которые входят в состав соединения -- сверхпроводника могут сверхпроводниками не являться.
Уменьшение сопротивления происходит очень резко в интервале нескольких сотых градуса.
Свойства сверхпроводников
1. В сверхпроводниках один раз возбужденный электрический ток может существовать без источника тока длительное время. Так как из-за отсутствия сопротивления время затухания тока становится очень большим.
2. Внутри вещества в сверхпроводящем состоянии магнитная индукция всегда равна нулю. Допустим, что тело их сверхпроводника охладили и перевели в сверхпроводящее состояние. Включили внешнее магнитное поле, индукция которого (без тела) равна:
При включении магнитного поля в сверхпроводнике появятся индукционные токи, которые порождают дополнительную индукцию равную:
которая по закону Ленца будет компенсировать внешнюю индукцию ${\overrightarrow{B}}_a.$ В обычном проводнике индукционные токи быстро затухают, остается только поток, который вызван намагничивающей катушкой. В сверхпроводнике компенсирующие токи не затухают, следовательно, суммарная индукция тела все время будет равна:
Во внешнем пространстве линии результирующей индукции будут выталкиваться из тела, и огибать его.
Сверхпроводящее вещество является идеальным диамагнетиком с магнитной восприимчивостью $\varkappa =-1$ и магнитной проницаемостью равной $\mu =1+\varkappa =0.$ Из этого следует, что плотность тока в толще массивного сверхпроводника равна нулю. В сверхпроводящем сплошном теле ток может находиться только в тонком слое поверхности.
3. Магнитное поле разрушает состояние сверхпроводимости. При увеличении напряженности магнитного поля выше определенного значения сверхпроводимость разрушается. Сверхпроводник становится просто проводником, а магнитное поле проникает внутрь вещества. Магнитное поле, при котором это происходит, называют критическим полем. Чем ниже температура сверхпроводника, чем больше при этом разрыв между температурой перехода в состояние сверхпроводимости и температурой вещества в данный момент, тем больше магнитное поле при котором исчезает сверхпроводимость. При температуре перехода в сверхпроводящее состояние критическое магнитное поле равно нулю.
Магнитное поле тока в сверхпроводнике может разрушить его сверхпроводимость.
В 1935 г. братья Лондоны нашли, что магнитное поле (H) проникает внутрь сверхпроводника и падает в зависимости от глубины по закону:
где ${\lambda }_L=\sqrt{\frac{m_ec^2}{4\pi n_Sq^2_e}}$ -- глубина проникновения магнитного поля в сверхпроводник, $n_S-\ $концентрация электронов проводимости. Для чистых металлов глубина проникновения примерно около ${\lambda }_L\sim {10}^{-5}см.$
Классификация сверхпроводников
Поверхностная энергия, связанная с наличием границ раздела между нормальной и сверхпроводящей фазами. Поверхностная энергия у сверхпроводников может быть как больше, так и меньше нуля. Сверхпроводники, для которых поверхностная энергия положительна, называются сверхпроводниками первого рода. Сверхпроводники с отрицательной поверхностной энергией - сверхпроводники второго рода.
На диаграмме состояния сверхпроводника 1 рода существуют только две области: сверхпроводящая и нормальная. На диаграмме состояний сверхпроводника второго рода присутствуют три области: сверхпроводящая, область смешанного состояния, нормальная область (рис.1). Кривая равновесия имеет параболическую форму. На этой кривой находятся критические точки ($B_k,\ T_k$). Из этих кривых видно, что магнитное поле понижает критическую температуру перехода в сверхпроводящее состояние.
Границы между областями на рис.1 определяют «нижнее» $B_{k1}$ и верхнее $B_{k2}$ критические поля. $T{\ }_{k0}$ -- критическая температура перехода в сверхпроводящее состояние, если внешнее магнитное поле равно нулю.
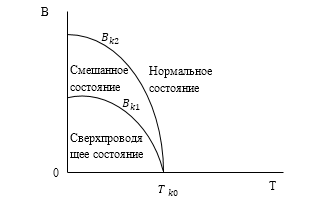
Рисунок 1.
Сверхпроводники второго рода используют в качестве соленоидов, в которых получают сильные магнитные поля. Сверхпроводники первого рода для этого не применимы, так как имеют низке значения критических магнитных полей.
Задание: Сверхпроводник имеет форму бесконечно длинного цилиндра (длинная проволока). Сила тока в проволоке равна I. Как индукция магнитного поля изменяется с расстоянием от оси проводника?
Решение:
В том случае, если тело имеет форму бесконечно длинного цилиндра, то напряженность магнитного поля во внешнем пространстве будет определяться полной силой тока:
\[H=\frac{I}{2\pi r}\left(1.1\right),\]где $r$ -- расстояние от оси провода, причем $r\ge R$, где $R$ -- радиус провода. Индукция связана с напряженностью магнитного поля выражением:
\[B={\mu }_0H\ \left(1.2\right).\]При переходе внутрь провода В по экспоненциальному закону уменьшается до нуля. Изменение индукции изображено на рис.2. Расстояние ${\lambda }_L$ от поверхности, при котором индукция магнитного поля уменьшается в e раз, называют ее глубиной проникновения. Глубина проникновения увеличивается при увеличении температуры.
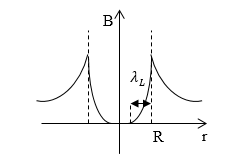
Рисунок 2.
Задание: Опишите физическую природу сверхпроводимости.
Решение:
Основой всех особенностей поведения сверхпроводника является свободное (без столкновений) движение внутри вещества носителей заряда. Этот эффект является чисто квантовым.
Между электронами металла действуют силы отталкивания, которые возникают согласно закону Кулона. Это взаимодействие существенно ослабляется экранирующим действием ионов кристаллической решетки. Электроны притягиваются к ионам, сила притяжения крайне мала, но при определённых условиях притяжение может превзойти отталкивание. В таком случае электроны образуют пары (их называют куперовскими), эти пары имеют нулевой спин, ведут себя как бозе -- частицы и являются носителями тока в сверхпроводниках. Размер пар довольно велик, он достигает порядка микрон.











