Средним ускорением $\left\langle a\right\rangle $ называется отношение приращения скорости $\triangle v=v\left(t+\triangle t\right)-v\left(t\right)\ $ к длительности промежутка времени $\triangle t$, в течение которого оно произошло: $\left\langle a\right\rangle =\frac{\triangle v}{\triangle t}$
Мгновенным ускорением $\overrightarrow{a}$ (или просто ускорением) тела называют предел отношения малого изменения скорости $\triangle \overrightarrow{v}$ малому промежутку времени $\Delta $t, в течение которого происходило изменение скорости:
В декартовых координатах это уравнение эквивалентно системе трёх уравнений:
Модуль вектора ускорения
Конец вектора скорости $\overrightarrow{v}$ при движении материальной точки описывает кривую, называемую годографом скорости (рис.2).
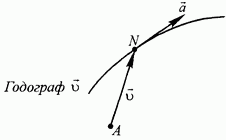
Рисунок 1. Годограф скорости
Ускорение в каждой точке годографа скорости направлено по касательной к годографу в этой точке. Следовательно, направление вектора ускорения $\overrightarrow{a}$ в случае криволинейного движения не совпадает с направлением вектора скорости $\overrightarrow{v}$.
Вектор мгновенного ускорения $\overrightarrow{a}$ можно представить как векторную сумму двух векторов, один из которых направлен по касательной к траектории в данной её точке, а другой -- перпендикулярен ему и направлен к центру кривизны траектории в этой точке.
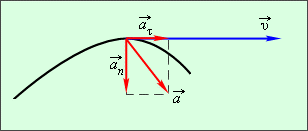
Рисунок 2. Касательное и нормальное ускорения
Эти составляющие вектора ускорения $\overrightarrow{a}$ называют касательным (тангенциальным) $\overrightarrow{a_{\tau }}={\mathop{lim}_{t\to 0} \frac{\triangle \overrightarrow{v_{\tau }}}{\triangle t}\ }$ и нормальным $\overrightarrow{a_n}={\mathop{lim}_{t\to 0} \frac{\triangle \overrightarrow{v_n}}{\triangle t}\ }$ ускорениями:
Касательное ускорение $\overrightarrow{a_{\tau }}$ указывает, насколько быстро изменяется скорость тела по модулю, а нормальное ускорение $\overrightarrow{a_n}$ указывает, насколько быстро скорость тела изменяется по направлению.
Из рис. 2 видно, что модуль полного ускорения $a=\sqrt{a^2_{\tau }+a^2_n}$
Криволинейное движение можно представить как движение по дугам окружностей (рис. 1.1.6).
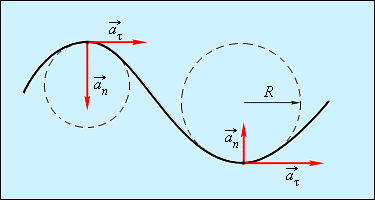
Рисунок 3. Движение по дугам окружностей
Нормальное ускорение $\overrightarrow{a_n}$ зависит от модуля скорости $\upsilon $ и от радиуса R окружности, по дуге которой тело движется в данный момент: $a_n= \frac{v^2}{R}$. Вектор $\overrightarrow{a_n}$ всегда направлен к центру окружности.
Определить скорость, ускорение и координату x точки в момент времени, равный 10 c, если уравнение движения материальной точки имеет вид $x=A+Bt+Ct^2$ , где А= 8 м, В = 5 м/c, С = 2 м/c2.
Дано: $x=A+Bt+Ct^2$;
А = 8 м; В = 5 м/с; С = 2 м/с2; t = 10 c. Найти: v --- ?, a --- ?, x --- ?
Решение:
Определяем координату x в заданный момент времени, подставив в уравнение движения материальной точки значения коэффициентов:
Определяем мгновенную скорость v материальной точки, как первую производную координаты по времени, и находим скорость материальной точки в заданный момент времени: $v=\dot{x}=B+2Ct=5+2\times 2\times 10=45\ м/с$
Определяем ускорение a материальной точки, как первую производную от скорости по времени и находим ускорение материальной точки в заданный момент времени:
Ответ: В момент времени t = 10 c координата материальной точки х = 238 м, скорость материальной точки v = $45\ м/с$ , ускорение материальной точки а = $20\ м/с^2$
Космический корабль движется в открытом космосе со скоростью $\overrightarrow{V}$. Требуется изменить направление скорости на 90 градусов, оставив величину скорости неизменной. Найдите минимальное время, необходимое для такого манёвра, если двигатель может сообщать кораблю в любом направлении ускорение, не превышающее $a$. По какой траектории будет при этом двигаться корабль?
Решение:
Перейдём в инерциальную систему отсчёта, движущуюся с постоянной скоростью $\overrightarrow{V}$. Так как во всех инерциальных системах отсчёта при одинаковых начальных условиях все механические явления протекают одинаково (принцип относительности Галилея), то ограничение, наложенное в условии задачи на ускорение корабля, не изменится. В новой системе отсчёта начальная скорость космического корабля равна нулю, а конечная скорость по модулю равна $v\sqrt{2}$ и направлена под углом к первоначальному направлению движения.
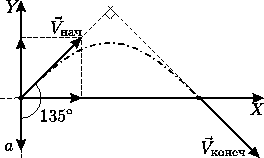
Теперь ясно, что для совершения манёвра нужно включить двигатели так, чтобы при развороте корабля его ускорение было всё время направлено в сторону конечной скорости корабля, то есть под углом 45 градусов к первоначальному направлению движения. Тогда минимальное время манёвра будет равно $\tau =\frac{\triangle v}{a}=\frac{V\sqrt{2}}{a}$.
Выясним, по какой траектории будет двигаться корабль при манёвре. Для этого вернёмся в исходную систему отсчёта и направим координатную ось декартовой системы координат в направлении, обратном ускорению, а ось $X$ --- перпендикулярно к ней, так, как показано на рисунке. Тогда закон движения в проекциях на эти оси примет вид:
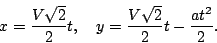
Выражая из первого уравнения время и подставляя его во второе, получим уравнение траектории корабля: $y=x-\frac{ax^2}{V^2}$ , то есть корабль будет двигаться по параболе, аналогично телу, брошенному по углом к горизонту.
Ответ: минимальное время, необходимое для манёвра $\tau =\frac{V\sqrt{2}}{a}$. Корабль в ходе манёвра будет двигаться по параболе.











