Движение точки М (или тела) $\overrightarrow{r}$ по отношению к основной системе координат называется абсолютным движением. Движение точки М (или тела) $\overrightarrow{{\mathbf \rho }}$ по отношению к подвижной системе координат называется относительным движением. Переносным называется движение ${\overrightarrow{r}}_O$ подвижной системы координат относительно основной, неподвижной. Абсолютная скорость $\overrightarrow{v}=\frac{d\overrightarrow{r}}{dt}$ и абсолютное ускорение $\overrightarrow{a}=\frac{d\overrightarrow{v}}{dt}$ точки M - это скорость и ускорение точки M в основной системе координат.
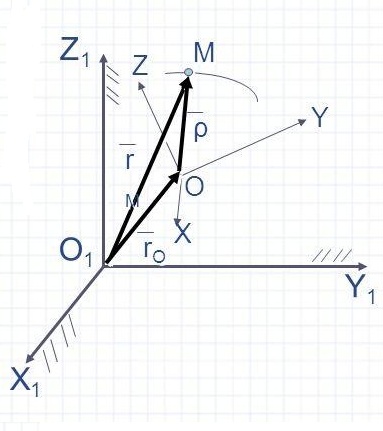
Рисунок 1. Переносное и относительное движение
Закон сложения скоростей
Вектор скорости материальной точки (тела) относительно неподвижной системы отсчёта $\overrightarrow{v}=\frac{d\overrightarrow{r}}{dt}={\overrightarrow{v}}_{АБС}$ (абсолютная скорость) является суммой вектора скорости тела относительно подвижной системы отсчета ${\overrightarrow{v}}_r=\frac{d\overrightarrow{{\mathbf \rho }}}{dt}={\overrightarrow{v}}_{ОТН}$ (относительной скорости) и вектора скорости подвижной системы отсчёта относительно неподвижной ${\overrightarrow{v}}_е=\frac{d\overrightarrow{r_O}}{dt}={\overrightarrow{v}}_{ПЕР}$ (переносной скорости):
\[{\overrightarrow{v}}_{АБС}={\overrightarrow{v}}_{ОТН}+{\overrightarrow{v}}_{ПЕР}\]Данный закон сложения скоростей справедлив только при скоростях, много меньших скорости света в вакууме. При релятивистских скоростях он имеет другую форму.
Если подвижная система отсчёта является вращающейся, то под переносной скоростью понимается скорость той точки подвижной системы отсчёта, в которой в данный момент находится тело.
Аналогично можно сформулировать и закон сложения ускорений для случая поступательного движения тела относительно подвижной системы отсчёта и подвижной системы отсчёта относительно неподвижной:
Закон сложения ускорений для поступательного движения
При поступательном движении тела относительно подвижной системы отсчёта и подвижной системы отсчёта относительно неподвижной, вектор ускорения материальной точки (тела) относительно неподвижной системы отсчёта $\overrightarrow{a}=\frac{d\overrightarrow{v}}{dt}=\ {\overrightarrow{a}}_{АБС}$ (абсолютное ускорение) является суммой вектора ускорения тела относительно подвижной системы отсчета ${\overrightarrow{a}}_r=\frac{d{\overrightarrow{v}}_r}{dt}={\overrightarrow{a}}_{ОТН}$ (относительного ускорения) и вектора ускорения подвижной системы отсчёта относительно неподвижной ${\overrightarrow{a}}_е=\frac{d{\overrightarrow{v}}_е}{dt}={\overrightarrow{a}}_{ПЕР}$ (переносного ускорения):
\[{\overrightarrow{a}}_{АБС}={\overrightarrow{a}}_{ОТН}+{\overrightarrow{a}}_{ПЕР}\]В общем случае, когда движение материальной точки (тела) является криволинейным, его в каждый момент времени можно представить как комбинацию поступательного движения материальной точки (тела) относительно подвижной системы отсчёта со скоростью ${\overrightarrow{v}}_r$, и вращательного движения подвижной системы отсчёта относительно неподвижной с угловой скоростью ${\overrightarrow{\omega }}_e$. В этом случае, при сложении ускорений, наряду с относительным и переносным ускорением необходимо учитывать и ускорение Кориолиса $a_c=2{\overrightarrow{\omega }}_e\times {\overrightarrow{v}}_r$, которое характеризует изменение относительной скорости, вызванное переносным движением, и изменение переносной скорости, вызванное относительным движением.
Теорема Кориолиса
Вектор ускорения материальной точки (тела) относительно неподвижной системы отсчёта $\overrightarrow{a}=\frac{d\overrightarrow{v}}{dt}=\ {\overrightarrow{a}}_{АБС}$ (абсолютное ускорение) является суммой вектора ускорения тела относительно подвижной системы отсчета ${\overrightarrow{a}}_r=\frac{d{\overrightarrow{v}}_r}{dt}={\overrightarrow{a}}_{ОТН}$ (относительного ускорения), вектора ускорения подвижной системы отсчёта относительно неподвижной ${\overrightarrow{a}}_е=\frac{d{\overrightarrow{v}}_е}{dt}={\overrightarrow{a}}_{ПЕР}$ (переносного ускорения), и кориолисова ускорения $a_c=2{\overrightarrow{{\mathbf \omega }}}_e\times {\overrightarrow{v}}_r={\overrightarrow{a}}_{КОР}$:
\[{\overrightarrow{a}}_{АБС}={\overrightarrow{a}}_{ОТН}+{\overrightarrow{a}}_{ПЕР}+{\overrightarrow{a}}_{КОР}\]Вторая капля оторвалась от крыши через несколько секунд после того, как оторвалась первая капля. Как движется вторая капля относительно первой? Сопротивлением воздуха пренебречь.
Решение
За неподвижную систему отсчёта возьмём землю, за подвижную систему отсчёта -- первую каплю, а за наблюдаемое тело -- вторую каплю. Отметим, что подвижная система отсчета движется поступательно. Поскольку сопротивлением воздуха пренебрегаем, то на каждую из капель будет действовать лишь одна сила тяжести, сообщающая каждой капле ускорение (относительно земли), равное ускорению свободного падения g. Следовательно, абсолютное ускорение (ускорение второй капли относительно земли) равно g, и переносное ускорение (ускорение первой капли относительно земли) также равно g. По закону сложения ускорений, относительное ускорение (ускорение второй капли относительно первой) равно нулю, значит, вторая капля движется равномерно относительно первой.
Ответ: вторая капля движется относительно первой равномерно.
Жесткий диск вращается с постоянной угловой скоростью $\overrightarrow{{\mathbf \omega }}$ вокруг оси, укрепленной на столе. По диску движется точка А с постоянной относительно стола скоростью $\overrightarrow{v}$. Определить скорость ${\overrightarrow{v}}_r$ и ускорение ${\overrightarrow{a}}_r$ частицы А относительно диска в момент, когда радиус-вектор, характеризующий ее положение по отношению к оси вращения, равен $\overrightarrow{{\mathbf \rho }}$.
Решение
Относительная скорость точки А $\ {\overrightarrow{v}}_r=\overrightarrow{v}-{\overrightarrow{{\mathbf \omega }}}_e\times \overrightarrow{{\mathbf \rho }}$.
Поскольку скорость точки $\overrightarrow{v}$ относительно стола постоянна, то её абсолютное движение равномерно, и $\overrightarrow{a}=0$
Отсюда
\[{\overrightarrow{a}}_r=-\left({\overrightarrow{a}}_e+{\overrightarrow{a}}_c\right)=-\left(2{\overrightarrow{{\mathbf \omega }}}_e\times {\overrightarrow{v}}_r+{{\mathbf \omega }}^2\overrightarrow{{\mathbf \rho }}\right)=2\overrightarrow{v}\times {\overrightarrow{{\mathbf \omega }}}_e-{{\mathbf \omega }}^2\overrightarrow{{\mathbf \rho }}\]










