В 1632 г. в книге «Диалог о двух главнейших системах мира - Птолемеевой и Коперниковой» Галилей обосновал принцип относительности, ставший одним из первых основных принципов физики.
Все ИСО по своим механическим свойствам эквивалентны друг другу.
Это значит, что никакими механическими опытами, проводимыми внутри данной ИСО, нельзя установить, покоится эта система или движется равномерно и прямолинейно. Этот принцип является обобщением опыта и подтверждается всем многообразием приложений механики Ньютона к движению тел, скорости которых значительно меньше скорости света.
Все сказанное достаточно ясно свидетельствует об исключительности свойств ИСО, в силу чего именно эти системы должны, как правило, использоваться для изучения механических явлений.
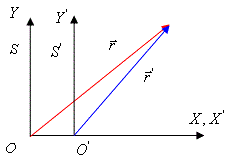
Рисунок 1. Инерциальные системы отсчёта
Найдем формулы преобразования координат при переходе от одной ИСО к другой. Допустим, что система отсчета S инерциальна. Рассмотрим вторую систему отсчета S', движущуюся относительно первой поступательно с постоянной скоростью ${\overrightarrow{v}}_0$ (рис. 1). Свяжем с каждой системой отсчета декартову систему координат. Для простоты можно принять, что координатные оси системы S соответственно параллельны координатным осям системы S' и что в начальный момент t0 = 0 начало О системы координат, связанной с системой отсчета S, совпадает с началом О' системы координат, связанной с системой отсчета S'. Кроме того, предположим, что скорость $\overrightarrow{v}$ параллельна оси OX. При этих условиях ось OХ будет все время совпадать с осью ОХ'.
Пусть в момент времени $t_0$ = 0 движущаяся точка находится в положении M. За время t начало координат ИСО S' переходит из точки О в положение О', причем, так как ${\overrightarrow{v}}_0=const$, то то $\overrightarrow{r}={\overrightarrow{r}}'+{\overrightarrow{v}}_0t'$, $t=t'$, где $\overrightarrow{r}$ и ${\overrightarrow{r}}'$ - радиус-векторы движущейся точки соответственно в системах отсчета $S\ $ и $S'$.
В проекциях на оси координат получим:
$\left\{ \begin{array}{c} x=x'+v_0t' \\ y=y' \\ z=z' \\ t=t' \end{array} \right.$
Формулы обратного преобразования имеют вид:
${\overrightarrow{r}}'=\overrightarrow{r}-{\overrightarrow{v}}_0t,\ t'=t$, или в координатной форме: $\left\{ \begin{array}{c} x'=x-v_0t \\ y'=y \\ z'=z \\ t'=t \end{array} \right.$
Эти формулы называются преобразованиями Галилея. Мы присоединили к формулам преобразования координат дополнительное выражение $t=t'$, чтобы явно отметить, что время в механике Ньютона считается абсолютным (то есть не меняется при переходе от одной системы отсчета к другой), и поэтому не преобразуется.
С точки зрения «здравого смысла» преобразования Галилея кажутся очевидными. Однако в основе вывода лежит предположение механики Ньютона об абсолютности длин и промежутков времени. Абсолютность времени явно отмечена в уравнении $t=t'$, при выводе остальных формул использовалось предположение об абсолютности длин.
Чтобы получить формулы сложения скоростей в нерелятивистской механике, возьмем производную по времени: $\frac{d\overrightarrow{r}}{dt}=\frac{d\overrightarrow{r}'}{dt}+{\overrightarrow{v}}_0=\frac{d\overrightarrow{r}'}{dt'}+{\overrightarrow{v}}_0$, или $\overrightarrow{v}={\overrightarrow{v}}'+{\overrightarrow{v}}_0$, где $\overrightarrow{v}$ -- скорость точки в системе отсчета S, а ${\overrightarrow{v}}'$ - в системе отсчета $S'$. Эта формула выражает закон сложения скоростей в классической механике. Повторное дифференцирование приводит нас к равенству ускорений тела в любой ИСО: $\overrightarrow{a}=\frac{d\overrightarrow{v}}{dt}=\frac{d\overrightarrow{v}'}{dt}=\frac{d\overrightarrow{v}'}{dt'}=\overrightarrow{a}'$, где $\overrightarrow{a}$ - ускорение точки в системе отсчета S, $\overrightarrow{a}'$ -- в системе отсчета S' Таким образом, ускорение точки в обеих системах отсчета одинаково. Говорят, что ускорение инвариантно относительно преобразований Галилея.
По определению ИСО, свободная материальная точка движется в системе отсчета S без ускорения. Поэтому движение данной материальной точки в системе отсчета S' будет также неускоренным. Следовательно, S' - также инерциальная система отсчета. Таким образом, система отсчета, движущаяся относительно инерциальной системы отсчета прямолинейно и равномерно, также является инерциальной системой. Следовательно, если существует хотя бы одна ИСО, то существует и бесконечное множество ИСО, движущихся относительно друг друга равномерно и прямолинейно.
Сила в классической механике зависит от ускорения, которое она сообщает телу. Поэтому, как видно из преобразований Галилея, она не меняется при переходе от одной системы отсчета к другой. Отсюда следует, что уравнение, выражающее второй закон Ньютона, остается неизменным при переходе от одной ИСО к другой. Такие уравнения называются инвариантными. Таким образом, уравнения механики Ньютона инвариантны относительно преобразований Галилея. Это утверждение и составляет содержание принципа относительности Галилея. Равноправие ИСО дает возможность в каждом конкретном случае подбирать систему отсчета, наиболее удобную для решения рассматриваемой задачи.
Движение происходит вдоль оси ОХ и соответственно закон преобразования (сложения) скоростей записывается через проекции скоростей на ось ОХ:
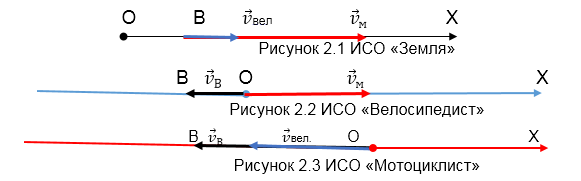
Ответ:

Лодка с мотором движется из точки А в точку В, которая находится на другом берегу реки (Рис. 3), скорость лодки относительно Земли неизменна по направлению. Расстояние АВ равно 100 м. Ширина реки равна 80 м. Скорость лодки относительно воды равна 1 м/с. Скорость воды в реке равна 1 м/с. Найти время переправы через реку.
Решение
Дано:
АВ = 100 м
$L$ = 80 м
$v_лодки$ = 1 м/с
$v_течения$ = 1 м/с
${\mathbf \Delta }$t - ?
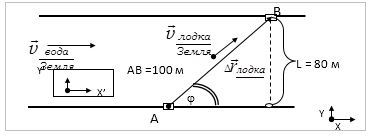
Рисунок 3
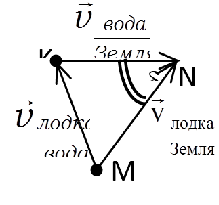
Рисунок 4
Имеем неподвижную ИСО, связанную с землёй, и подвижную ИСО, связанную с течением реки. ${\overrightarrow{v}}_{\frac{лодка}{земля}}={\overrightarrow{v}}_{\frac{лодка}{вода}}+{\overrightarrow{v}}_{\frac{вода}{земля}}$ , а время переправы $\triangle t=\frac{\triangle \overrightarrow{r}}{\left|{\overrightarrow{v}}_{\frac{лодка}{земля}}\right|}=\frac{AB}{\left|{\overrightarrow{v}}_{\frac{лодка}{земля}}\right|}$ . Поскольку в треугольнике скоростей МKN $\delta =\varphi =arc{sin \frac{L}{AB}\ }$ и $\left|{\overrightarrow{v}}_{\frac{лодка}{вода}}\right|=\left|{\overrightarrow{v}}_{\frac{вода}{земля}}\right|=1\ м/с$, то $\widehat{МКN}=180{}^\circ -2\varphi \ $; \[{cos \widehat{MKN}=-{cos 2\varphi \ }\ }=-\left(1-2{sin}^2\varphi \right)=-\left(1-2{\left(\frac{L}{AB}\right)}^2\right)\] $\left|{\overrightarrow{v}}_{\frac{лодка}{земля}}\right|=\sqrt{{\left|{\overrightarrow{v}}_{\frac{лодка}{вода}}\right|}^2+{\left|{\overrightarrow{v}}_{\frac{вода}{земля}}\right|}^2-2\ \left|{\overrightarrow{v}}_{\frac{лодка}{вода}}\right|\cdot \left|{\overrightarrow{v}}_{\frac{вода}{земля}}\right|\cdot {cos \widehat{МКN}\ }}=1,2\ м$/c; $\triangle t=\frac{100}{1.2}=83\ c$.Ответ: время переправы 83 с












