Движение точки в пространстве можно считать заданным, если известны законы изменнеия трех ее декартовых координат x, y, z как функции времени. Однако в некоторых случаях пространственного движения материальных точек (например, в областях, ограниченных поверхностями различной формы) использование уравнений движения в декартовых координатах неудобно, так как они становятся слишком громоздкими. В таких случаях можно выбрать другие три независимых скалярных параметра $q_1,{\ q}_2,\ \ q_3$, называемых криволинейными, или обобщенными координатами, которые также однозначно определяют положение точки в пространстве.
Скорость точки М при задании ее движения в криволинейных координатах определится в виде векторной суммы составляющих скоростей, параллельных координатным осям:
\[\overrightarrow{v}=\frac{d\overrightarrow{r}}{dt}=\frac{\partial \overrightarrow{r}}{\partial q_1}\dot{q_1}+\frac{\partial \overrightarrow{r}}{\partial q_2}\dot{q_2}+\frac{\partial \overrightarrow{r}}{\partial q_3}\dot{q_3}=v_{q_1}\overline{e_1}+v_{q_2}\overline{e_2}\ +v_{q_3}\overline{e_3}\]Проекции вектора скорости на соответствующие координатные оси равны: $v_{q_i}=\overline{v\ }\cdot \overline{e_i}=H_i\dot{q_i}\ \ ,\ \ i=\overline{1,3}$
Здесь $H_i=\left|{\left(\frac{\partial \overrightarrow{r}}{\partial q_i}\right)}_M\right|$ - параметр, который называется i-м коэффициентом Ламе и равен значению модуля частной производной от радиус-вектора точки по i-ой криволинейной координате, вычисленной в данной точке М. Каждый из векторов $\overline{e_i}$ имеет направление, соответствующее направлению движения точки конца радиус-вектора $r_i$ при возрастании i-й обобщенной координаты. Модуль скорости в ортогональной криволинейной системе координат можно рассчитать по зависимости:
\[v=\sqrt{v^2_{q_1}+v^2_{q_2}+v^2_{q_3}}=\sqrt{H^2_1{\dot{q_1}}^2+H^2_2{\dot{q_2}}^2+H^2_3{\dot{q_3}}^2}\]В приведенных формулах значения производных и коэффициентов Ламе вычисляют для текущего положения точки М в пространстве.
Координатами точки в сферической системе координат являются скалярные параметры r, ${\mathbf \varphi },\ {\mathbf \theta }$, отсчитываемые так, как показано на рис. 1.
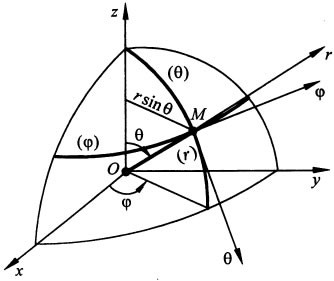
Рисунок 1. Вектор скорости в сферической системе координат
Система уравнений движения точки в данном случае имеет вид:
\[\left\{ \begin{array}{c} r=r(t) \\ \varphi =\varphi (t \\ \theta =\theta (t \end{array} \right.\]На рис. 1 изображены радиус-вектор r, проведенный из начала координат, углы ${\mathbf \varphi }$ и ${\mathbf \theta }$, а также координатные линии и оси рассматриваемой системы в произвольной точке М траектории. Видно, что координатные линии $({\mathbf \varphi })$ и $({\mathbf \theta })$ лежат на поверхности сферы радиусом r. Данная криволинейная система координат также является ортогональной. Декартовы координаты могут быть выражены через сферические координаты так:
\[x=rcos\varphi sin\theta ;\ \ y=rsin\varphi cos\theta ;\ \ z=rcos\theta \ \ \]Тогда коэффициенты Ламе: $H_r=1;\ \ H_{\varphi }=rsin\varphi ;\ \ H_0=r$ ; проекции скорости точки на оси сферической системы координат $v_r=\dot{r\ \ };$ $v_{\theta }=r\dot{\theta }$; $\ v_{\varphi }=r\dot{\varphi }sin\theta $, а модуль вектора скорости
\[v=\sqrt{v^2_r+v^2_{\varphi }+v^2_{\theta }}=\sqrt{{\dot{r}}^2+r^2{\dot{\varphi }}^2+r^2{\dot{\theta }}^2}\]Ускорение точки в сферической системе координатат
\[\overrightarrow{a}=a_r{\overrightarrow{e}}_r+a_{\varphi }{\overrightarrow{e}}_{\varphi }+a_{\theta }{\overrightarrow{e}}_{\theta },\]проекции ускорения точки на оси сферической системы координат
\[a_r=\dot{r}-r\left({\dot{\theta }}^2+{\dot{\varphi }}^2{sin}^2\varphi \right); a_{\varphi }=r\ddot{\varphi }{sin \varphi \ }+2r\dot{\varphi }\left({sin \theta \ }+\dot{\theta }{cos \theta \ }\right);\] \[a_{\theta }=r\ddot{\theta }-r{\dot{\varphi }}^2{sin \theta \ }{cos \theta \ }+2\dot{r}\dot{\theta }\]Модуль ускорения $a=\sqrt{a^2_r+a^2_{\varphi }+a^2_{\theta }}$
Точка движется по линии пересечения сферы и цилиндра согласно уравнениям: r = R, $\varphi $ = kt/2, $\theta $ = kt/2 , (r, $\varphi $, $\theta $ --- сферические координаты). Найти модуль и проекции скорости точки на оси сферической системы координат.
Решение
Найдём проекции вектора скорости на оси сферических координат:
\[v_r=\dot{r}=0;;\ \ v_{\varphi }=r\dot{\varphi }sin\theta =R\frac{k}{2}{sin \frac{kt}{2}\ };;\ \ \ v_{\theta }=r\dot{\theta }=R\frac{k}{2}\]Модуль скорости $v=\sqrt{v^2_r+v^2_{\varphi }+v^2_{\theta }}=R\frac{k}{2}\sqrt{{sin}^2\frac{kt}{2}+1}$
Используя условие задачи 1, определить модуль ускорения точки.
Решение
Найдём проекции вектора ускорения на оси сферических координат:
\[a_r=\dot{r}-r\left({\dot{\theta }}^2+{\dot{\varphi }}^2{sin}^2\varphi \right)=R\frac{k^2}{4}\left(1+{sin}^2\frac{kt}{2}\right)\] \[a_{\varphi }=r\ddot{\varphi }{sin \varphi \ }+2r\dot{\varphi }\left({sin \theta \ }+\dot{\theta }{cos \theta \ }\right)=-R\frac{k^2}{2}{sin \frac{kt}{2}\ }\] \[a_{\theta }=r\ddot{\theta }-r{\dot{\varphi }}^2{sin \theta \ }{cos \theta \ }+2\dot{r}\dot{\theta }=-R\frac{k^2}{4}{sin \theta {cos \frac{kt}{2}\ }\ }\]Модуль ускорения $a=\sqrt{a^2_r+a^2_{\varphi }+a^2_{\theta }}=R\frac{k^2}{4}\sqrt{4+{sin}^2\frac{kt}{2}}$











