Тело или совокупность неподвижных одно относительно другого тел, относительно которой определяется пространственное и временное положение других тел, вместе с прибором для измерения времени называется системой отсчета.
С точки зрения кинематики все системы отсчета кинематически эквивалентны. В кинематике нельзя указать преимуществ одной системы отсчета по сравнению с другой. При решении задач кинематики ее выбор определяется соображениями целесообразности (удобства).
Для описания пространства, в котором осуществляется движение материальной точки, с системой отсчета связывают пространственную систему координат.
Система пространственных координат -- комплекс определений, реализующий метод координат, то есть способ определять положение точки или тела с помощью чисел или других символов. Совокупность чисел, определяющих положение конкретной точки в трёхмерном пространстве, называется координатами этой точки.
Под афинной системой координат понимают тройку линейно независимых векторов (координатных осей), выходящих из одной точки (начала отсчета).
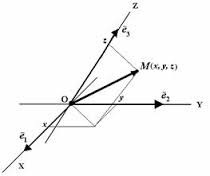
Рис.1 Положение точки в афинной системе координат.
В этом случае положение материальной точки М в пространстве определяется радиусом-вектором $\overrightarrow{r}$, проведенным из начала координат 0 в эту точку, а движение представляется в виде векторной суммы независимых движений вдоль трех пространственных осей выбранной системы координат.
Наиболее часто используется прямоугольная, декартова система координат, образованная тремя взаимно перпендикулярными осями X, Y, Z. Она наиболее пригодна для описания прямолинейного движения и движения по незамкнутым и нециклическим кривым, сочетает наглядность геометрической интерпретации с простотой вычислений.

Рис.2. Положение точки в декартовой системе координат.
Единичные вектора, отложенные из начала координат О вдоль координатных осей, называются ортами - $\overrightarrow{i;}\overrightarrow{j};\overrightarrow{k}$ . Положение произвольной точки M характеризуется радиус-вектором $\overrightarrow{r}$, соединяющим начало координат О с точкой М:
\[\overrightarrow{r}=x\overrightarrow{i}+y\overrightarrow{j}+z\overrightarrow{k}\]X, Y, Z -- декартовы координаты точки M, или проекции радиус-вектора на соответствующие оси координат. Характер движения тела в пространстве будет задан, если мы будем знать, как меняются во времени координаты или его радиус-вектор, т.е. будут определены зависимости x=x(t); y=y(t).
Для однозначного определения положения точки М в пространстве радиус-вектор $\overrightarrow{r}$ полагают зависящим от параметра t, называемого временем, так, что каждому значению t соответствует одно значение функции:
\[\overrightarrow{r}=\overrightarrow{r}\left(t\right)=x\left(t\right)\overrightarrow{i}+y\left(t\right)\overrightarrow{j}+z\left(t\right)\overrightarrow{k}\]Это равенство называется кинематическим уравнением движения точки М, записанным в векторной форме.
Для описания криволинейного движения, наряду с афинными, используются криволинейные системы координат, позволяющие в ряде случаев существенно упростить форму записи законов движения тел и облегчить вычисления. Наиболее употребительны цилиндрическая и сферическая системы координат.
Цилиндрическая система координат представляет собой трёхмерную систему координат, являющуюся обобщением полярной системы координат на трёхмерное пространство посредством добавления третьей координаты, которая задаёт смещение произвольной точки M вдоль оси ОZ относительно координатной плоскости OXY. Положение точки M в цилиндрической системе координат определяется тройкой скаляров $\rho $, $\varphi $ и z, где $\rho $ -- расстояние от точки M до оси OZ ()$;$ $\varphi $ -- угол, образованный проекцией радиус-вектора точки M на плоскость OXY с положительным направлением оси OX; z -- проекция точки M на ось OZ.
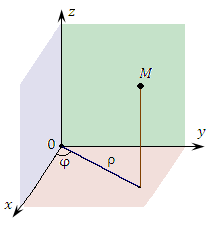
Рис. 3. Цилиндрические координаты точки M.
Связь между декартовыми и цилиндрическими координатами описывается формулами:
\[x=\rho cos\varphi ;\ \ \ y=\rho sin\varphi ;\ \ \ z=z;\ \ \ \rho =\sqrt{x^2+y^2};\ \ \ tg\varphi =\frac{y}{x}.\]В сферической системе координат тройку скалярных величин, определяющих положение точки в пространстве, составляют длина её радиус-вектора $\rho $ и два угла: $\varphi $ -- угол, образованный проекцией радиус-вектора точки M на плоскость OXY с положительным направлением оси OX (), и $\theta $ - угол между радиус-вектором точки M и осью ОZ.
Рассмотрим сферическую систему координат О${\mathbf \rho }{\mathbf \theta }{\mathbf \varphi }$, совмещённую с декартовой системой ОXYZ. При этом максимальные пределы изменения сферических координат таковы: 0 ≤ $\varphi $ ≤ 2$\pi $, 0 ≤ $\rho $ ≤ $ \infty $
Из рис. 4 нетрудно вывести следующие формулы, связывающие декартовые и сферические координаты:
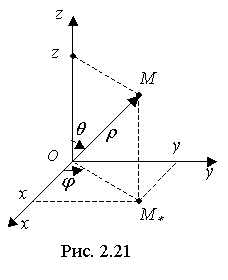
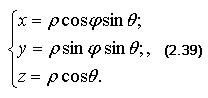
Рис.4. Сферические координаты точки М
Существуют и другие системы криволинейных координат: параболические, гиперболические, эллиптические и т.д.
Выбор системы отсчёта, то есть тела отсчёта и системы координат, в каждом конкретном случае определяется особенностями траектории движения тела, с таким расчётом, чтобы закон движения, записанный в этой системе координат, был как можно проще.











