Устойчивые и неустойчивые конфигурации зарядов
Для теории построения материи с точки зрения электричества немаловажным является вопрос об устойчивых и неустойчивых конфигурациях электрических зарядов. Все вещество состоит из нейтронов, электронов, протонов, последние два вида частиц несут заряд, следовательно, непраздным является вопрос о том, может ли система зарядов находится в состоянии устойчивого статического равновесия или в атомах и молекулах всех тел электроны и протоны должны непрерывно двигаться?
Рассмотрим систему точечных зарядов. Электрическая энергия (W) системы зарядов играет роль потенциальной энергии системы. Из механики мы знаем, что условием устойчивого равновесия является минимум потенциальной энергии, следовательно, в нашем случае, минимум энергии W. Энергия системы точечных зарядов равна:
где $r_{i,k}=\sqrt{{(x_i-x_k)}^2+{(y_i-y_k)}^2{(z_i-z_k)}^2}$ -- функция координат зарядов системы. Мы знаем, что функция W будет иметь минимум, если первые производные по всем координатам всех зарядов были равны нулю и вторые производные от W по координатам ${x(}_{h,}y_h{,z}_h\ ;\ h-любое)\ $были больше нуля. Мы имеем:
где ${\overrightarrow{\nabla }}_h=\frac{\partial }{\partial x_h}\overrightarrow{i}+\frac{\partial }{\partial y_h}\overrightarrow{j}+\frac{\partial }{\partial z_h}\overrightarrow{k}$ - оператор набла для заряда $q_h$. Очевидно, что при$\ h\ne i,\ h\ne k$ получим, что:
но при $h=i,\ h=k$ выражение (3) равно нулю. Следовательно, мы получили, что:
Имеем то, что требование о существовании вторых производных от W больших нуля не выполняется. Получилось, что энергия W не может иметь минимум.
Из экспериментальных исследований известно, что расстояния между заряженными частицами, которые входят в составы атомов всех тел, довольно велико (${\approx 10}^{-10}м$) в сравнении с размерами самих частиц (${\approx 10}^{-14}м$). Поэтому каждый атом можно считать системой точечных зарядов. К такой системе применима теорема Ирншоу. С другой стороны атомы химических элементов являются устойчивыми системами. Значит, делаем вывод о том, что построение вещества из заряженных частиц в статическом состоянии не возможно, следовательно, атом представляет собой динамическую систему.
Идеальный проводник и идеальный диэлектрик
Итак, согласно теореме Ирншоу, чисто статистические электрические системы неустойчивы. Для того, чтобы избегать рассмотрения скрытого движения элементарных зарядов, макроскопическая электростатическая теория использует формальные представления о добавочных силах (связях не электростатического происхождения), которые обеспечивают необходимую устойчивость систем зарядов. В этом отношении существует аналогия электростатики и механики. В механике, как мы помним, применяются представления о связях, которые осуществляются с помощью опор, осей, нитей и т.д. И, если представления о связях в электростатике применяются, значит, развитием теории должно быть раскрытие физического смысла таких связей.
В электростатике довольно близким приближением к действительности является введение таких связей как: идеальный проводник и идеальный диэлектрик. Относительно проводников, например, мы всегда полагали, что на поверхности проводника существуют некие силы, которые не имеют электростатического происхождения, препятствуют выходу зарядов за пределы поверхности проводника. Только эти силы обеспечивают устойчивость системы заряженных проводников, в противном случае существование уединенного заряженного проводника было бы не возможно. Элементы его заряда под действием взаимоотталкивания разлетелись бы в бесконечность. Если использовать термины механики, то такие силы можно назвать -- реакциями связей.
Теорема Ирншоу является следствием теоремы Остроградского - Гаусса.
Задание: Имеется система из двух зарядов:
\[q_1=-4Q,\ q_2=-4Q.\]Какой заряд необходимо поместить между двумя имеющимися, чтобы системы находилась в равновесии? Где должен находиться искомый заряд?
Решение:
Расположим приведенные в условии заряды вдоль одной прямой рис. 1.
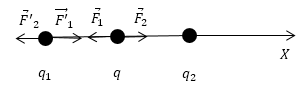
Рис. 1
Для равновесия электрических зарядов необходимо и достаточно, чтобы сила, которая действует на каждый заряд, обращалась, в нуль. Запишем силы, которые действуют на искомый заряд $q$:
\[{\overrightarrow{F}}_1+{\overrightarrow{F}}_2=0\ \left(1.1\right).\]По закону Кулона модули сил $F_1$=$F_2$ и равны:
\[F_1=k\frac{q_1q}{r^2}\left(1.2\right).\] \[F_2=k\frac{q_2q}{({l-r)}^2}(1.3).\]Приравняем (1.2) и (1.3), получим:
\[k\frac{q_1q}{r^2}=k\frac{q_2q}{({l-r)}^2}\to \frac{1}{r^2}=\frac{1}{({l-r)}^2}\to ({l-r)}^2=r^2\to l^2-2lr+r^2=r^2\to l^2-2lr=0\to l-2r=0\to r=\frac{l}{2}.\]Мы получили, что искомый заряд должен находиться посередине между заданными зарядами. Найдем величину искомого заряда, очевидно, что он должен иметь знак противоположный имеющимся зарядам. Рассмотрим силы, которые действуют на заряд $q_1$ со стороны остальных зарядов (рис.1):
\[{\overrightarrow{F'}}_1+{\overrightarrow{F'}}_2=0\ \left(1.4\right).\]Зная из закона Кулона, что:
\[{F'}_1=k\frac{q_1q}{r^2}\ \left(1.5\right).\] \[{F'}_2=k\frac{q_1q_2}{4r^2}\ \left(1.6\right).\]Приравниваем (1.5) и (1.6) исходя из (1.4), получим:
\[k\frac{q_1q}{r^2}=k\frac{q_1q_2}{4r^2}\to q=\frac{q_2}{4}=Q\]Ответ: Для того чтобы система из трех зарядов (два из которых заданы в условии), находилась в равновесии необходимо поместить третий заряд на равном расстоянии от каждого из имеющихся и величина заряда должна быть в четыре раза меньше, чем у исходных частиц.
Задание: Теорема Ирншоу является следствием теоремы Остроградского -- Гаусса. Докажите истинность теоремы Ирншоу, опираясь на теорему Остроградского -- Гаусса.
Решение:
Проведем доказательство от противного. Пусть некая система точечных зарядов находится в устойчивом равновесии. Рассмотрим один из произвольных зарядов q (допустим, что q$>$0) этой системы. Пусть он находится в точке 1. (рис. 2).
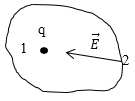
Рис. 2
Сместим заряд q из точки 1 в точку 2. Точки 1 и 2 бесконечно близкие. Если положение равновесия устойчиво, то возникнет сила, которая направлена в сторону точки 1, которая будет стремиться вернуть заряд в точку 1 из второй точки. Пусть $\overrightarrow E $ - электрическое поле, которое создают все имеющиеся в системе заряды за исключением заряда $q$. В точке 2 это поле должно иметь направление к точке 1, не зависимо от направления смещения $1\to 2$. Окружим заряд $q$ произвольной замкнутой поверхностью $S$ такой, чтобы все остальные заряды были расположены вне этой поверхности. На поверхности $S$ поле направлено к точке 1, следовательно, поток вектора через поверхность $S$ меньше нуля. Что противоречит теореме Остроградского -- Гаусса. Так как данная теорема требует, чтобы поток в этом случае был равен нулю, так как он создан зарядами, которые находятся вне полости $S$. Следовательно, мы доказали, что теорема Ирншоу справедлива.











