
Что такое свободные и связанные заряды
Когда мы рассматриваем диэлектрики в электростатических полях необходимо различать два вида электрических зарядов: свободные и связанные.
Свободными зарядами надо считать заряды, которые могут под действием поля перемещаться на существенные расстояния, как например, электроны в проводниках, ионы в газах и заряды, привнесенные извне на поверхность диэлектриков, которые нарушают их (диэлектриков) нейтральность. Заряды, которые входят в состав нейтральных, в целом, молекул диэлектриков, так же, как и ионы, которые закреплены в кристаллических решетках твердых диэлектриков около положений равновесия, называют связанными зарядами.
Потенциал электростатического поля в диэлектрике ($\varphi $) равен:
\[\varphi ={\varphi }_0+{\varphi }'\left(1\right),\]где ${\varphi }_0$ -- потенциал поля создаваемого свободными зарядами, ${\varphi }'$ - потенциал поля создаваемого связанными зарядами. При этом мы знаем, что:
\[{\varphi }_0=\int{\frac{\rho dV}{R}}+\int{\frac{\sigma dS}{R}}\left(2\right),\ \]где $\rho $ -- объемная плотность свободных зарядов, $\sigma $ -- поверхностная плотность свободных зарядов. Потенциал поля связанных зарядов определен как:
\[{\varphi }'=\int{\frac{\overrightarrow{P}\overrightarrow{R}}{R^3}}dV\left(3\right),\]где $\overrightarrow{P}$ -- вектор поляризации.
Из уравнений (1) и (3) следует, что:
\[\varphi ={\varphi }_0+\int{\frac{\overrightarrow{P}\overrightarrow{R}}{R^3}}\left(4\right).\]Если использовать теорему Остроградского - Гаусса и некоторые формулы векторного анализа, не сложно получить иной вид уравнения (4), а именно:
\[\varphi ={\varphi }_0+\int{\frac{{\rho }_{sv}}{R}dV}+\int{\frac{{\sigma }_{sv}}{R}dV=\int{\frac{{\rho }_{sv}+\rho }{R}dV}+\int{\frac{{\sigma }_{sv}+\sigma }{R}dV}}\left(5\right),\]где ${\rho }_{sv}$- средняя объемная плотность связанных зарядов, ${\sigma }_{sv}-средняя\ поверхностная\ плотность\ $ связанных зарядов. Из уравнения (5) видно, что электрическое поле при наличии диэлектрика совпадает с полем, которое создано свободными зарядами плюс поле, которое создается связанными зарядами.
Плотность связанных зарядов
При $\overrightarrow{P}=const$ (что означает равномерную поляризацию диэлектрика) средняя плотность связанных зарядов равна нулю, что означает, что в данном случае не происходит накопление зарядов одного знака в диэлектрике. На границе между поляризованным диэлектриком и вакуумом или металлом сосредоточен поверхностный связанный заряд плотности:
\[{\sigma }_{sv}=\pm P_n,\ -div\ \overrightarrow{P}={\rho }_{sv}\left(6\right),\]где $P_n$ -- нормальная компонента вектора поляризованности диэлектрика на его границе с вакуумом.
Функция $\varphi $ вида (7) является решением уравнения:
\[{\nabla }^2\varphi =-4\pi \left(\rho +{\rho }_{sv}\right)\left(7\right).\]Зная, что:
\[\overrightarrow{E}=-\nabla \varphi \ \to div\overrightarrow{E}=-{\nabla }^2\varphi (8)\]и учитывая (6), можно записать, что:
\[div\overrightarrow{E}=4\pi \rho -4\pi div\overrightarrow{P}\ (9)\]или
\[div\overrightarrow{(E}+4\pi \overrightarrow{P})=4\pi \rho \ \left(10\right).\]Уравнение (10) -- основное дифференциальное уравнение электростатического поля в любой произвольной среде.
Для того, чтобы получить полную систему уравнений электростатики к уравнению (10), необходимо добавить выражение, связывающее векторы напряженности электрического поля и вектор поляризации.
Зависимость $\overrightarrow{P}(\overrightarrow{E})$ в общем случае представлена в виде:
\[P_i={\varepsilon }_0\sum\limits_j{{\varkappa }_{ij}E_j+{\varepsilon }_0\sum\limits_{j,k}{{\varkappa }_{ijk}E_jE_k+\dots ,}\left(11\right),}\]где индексы $i,j$ -- нумеруют компоненты по осям декартовой системы координат $(i=x,\ y,z; j=x,\ y,z.)$, ${\varkappa }_{ij}$ -- тензор диэлектрической восприимчивости.
Итак, при наличии внешнего электрического поля вещество само становится источником поля, следовательно, поле изменяется.
Задание: Имеется плоский конденсатор, пространство между обкладками которого, заполнено однородным, изотропным диэлектриком c диэлектрической восприимчивостью $\varkappa$. На обкладках конденсатора находится поверхностный заряд, плотность его равна $\sigma .$ Какова напряженность результирующего поля в конденсаторе?
Решение:
Если между обкладками конденсатора вакуум, то напряженность поля, которое создают заряженные обкладки, равно:
\[E_{vak}=\frac{\sigma }{{\varepsilon }_0}\left(1.1\right),\]где ${\varepsilon }_0=8,\ 85\cdot {10}^{-12}\frac{Ф}{м}.\ $-- электрическая постоянная.
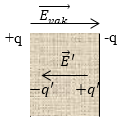
Рис. 1
$+q, -q$ -- заряды на обкладках конденсатора.
$\overrightarrow{E_{vak}}$ -- напряженность поля, которое создается обкладками конденсатора.
$-q', +q'$ -заряды диэлектрика.
$\overrightarrow{E}'$ - напряженность поля, которое создается в результате поляризации диэлектрика.
Так как диэлектрик поляризуется, напряженность поля уменьшается. Так как диэлектрик считаем однородным, поле, которое создается в плоском конденсаторе, также можно считать однородным, делаем вывод о том, что поляризованность диэлектрика однородна, то есть объемные связанные заряды отсутствуют (${\rho }_{sv}=0$). Имеем только поверхностные заряды плотность которых (${\sigma }_{sv}$):
\[{\sigma }_{sv}=P_n\ \left(1.2\right).\]Зная связь напряженности поля и вектора поляризации для изотропного диэлектрика:
\[P=\varkappa {\varepsilon }_0E(1.3)\]получим:
\[{\sigma }_{sv}=\varkappa {\varepsilon }_0E\left(1.4\right),\]где $E$ -- проекция напряженности на внешнюю нормаль к поверхности диэлектрика. Напряженность поля направлена от положительно заряженной пластины конденсатора к отрицательной. Поэтому из (1.4) следует, что поверхностная плотность связанного заряда на границе с положительно заряженной пластиной имеет знак минус, а на границе с отрицательной пластиной - плюс. Получаем, что напряженность поля в диэлектрике между пластинами конденсатора равна напряженности поля в вакууме между теми же пластинами, но при поверхностной плотности заряда равном:
\[{\sigma }'=\sigma -{\sigma }_{sv}\left(1.5\right).\]На этом основании запишем, что напряженность поля в конденсаторе при наличии диэлектрика равна:
\[E=\frac{\left(\sigma -{\sigma }_{sv}\right)}{{\varepsilon }_0}=\frac{\left(\sigma -\varkappa {\varepsilon }_0E\right)}{{\varepsilon }_0}\ \left(1.6\right).\]Выразим из (1.6) искомую напряженность:
\[E=\frac{\sigma }{{\varepsilon }_0(1+\varkappa )}.\]Ответ: $E=\frac{\sigma }{{\varepsilon }_0(1+\varkappa )}.$
Задание: Точечный заряд q окружён концентрическим слоем диэлектрика (рис.2). Найдите поверхностную плотность связанных зарядов, которые индуцированы точечным зарядом q, если известны радиусы $R_1\ и\ R_2$ (рис.2). Сферический слой заполнен диэлектриком с диэлектрической проницаемостью $\varepsilon .$
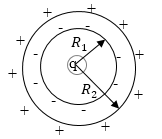
Рис. 2
Решение:
Напряженность поля точечного заряда будет иметь вид:
\[\left\{ \begin{array}{c} E_r=\frac{1}{4\pi {\varepsilon }_0}\frac{q}{r^2}\ при\ r Из (2.1) видим, что напряженность терпит разрыв на поверхности сферического слоя диэлектрика при $r=R_1$ и $r=R_2.$ Зная связь напряженности и вектора поляризации для изотропного диэлектрика и то, что при отсутствии диэлектрика связанных зарядов нет , соответственно вектор поляризации равен нулю получим: \[\left\{ \begin{array}{c} P_r=0\ при\ r Соответственно, поверхностная плотность связанных зарядов равна: \[{\sigma }_{sv1}=-P_r\left(r=R_1\right)=-\left(\frac{\varkappa }{4\pi \varepsilon }\frac{q}{{R_1}^2}\right),\] \[{\sigma }_{sv2}=P_r\left(r=R_2\right)=\left(\frac{\varkappa }{4\pi \varepsilon }\frac{q}{{R_2}^2}\right).\]Ответ: Поверхностные плотности индуцированных зарядов равны: ${\sigma }_{sv1}=-\left(\frac{\varkappa }{4\pi \varepsilon }\frac{q}{{R_1}^2}\right),$ ${\sigma }_{sv2}=\left(\frac{\varkappa }{4\pi \varepsilon }\frac{q}{{R_2}^2}\right)$.











