Что такое поляризуемость
Любая молекула есть система из положительных и отрицательных зарядов. Если диэлектрик поместить в электрическое поле, то оно вызовет смещение зарядов в молекуле, тем самым создаст индуцированный дипольный момент.
Свойство атома или молекулы приобретать дипольный момент во внешнем электрическом поле так же, как и количественная характеристика способности зарядов к смещению, называется поляризуемостью.
Некоторые вещества построены из молекул, в состав которых входят незаряженные атомы, например, молекула водорода. Неполярную молекулу в отсутствии внешнего поля можно уподобить в виде двух равномерно заряженных сфер, центры которых совпадают. Поле равномерно заряженной сферы во внешнем пространстве такое же, как поле точечного заряда той же величины, что и заряд сферы, помещенного в центр сферы. Электрический момент такой молекулы равен нулю. Если неполярная молекула попадает в электрическое поле, то заряды смещаются друг относительно друга в противоположные стороны. Молекула вызывает электрическое поле, которое совпадает (вне молекулы) с полем диполя. У такого диполя каждый из точечных зарядов равен заряду сферы, а плечо диполя равно расстоянию между центрами сфер.
Смещение зарядов в слабых полях можно считать пропорциональным напряженности внешнего электрического поля. При этом дипольный момент молекулы (${\overrightarrow{p}}_e$) можно считать равным:
\[\overrightarrow{p_e}=\beta {\varepsilon }_0\overrightarrow{E'}\left(1\right),\]где $\overrightarrow{E'}$ -- напряженность поля, действующего на молекулу (в жидкостях и газах $\overrightarrow{E'}\ne \overrightarrow{E}$, $\overrightarrow{E}$ -- среднее макроскопическое поле). Мы далее будем рассматривать газ, в нем $\overrightarrow{E'}=\overrightarrow{E}.$ $\beta $ -- коэффициент поляризуемость молекулы, величина, которая зависит от строения молекулы. Формула (1) применима к молекулам со сферической симметрией. Такой тип поляризации называют электронной поляризацией.
Пусть неполярный диэлектрик находится во внешнем поле, примем, что локальное поле равно среднему полю внутри диэлектрика, то есть $\overrightarrow{E'}=\overrightarrow{E}.$ В таком случае каждая молекула имеет дипольный момент $\overrightarrow{p_e}$ выраженный формулой (1). В таком случае вектор поляризованности имеет вид:
\[\overrightarrow{P}=n\beta {\varepsilon }_0\overrightarrow{E\ }\left(2\right),\]где $n$ - концентрация молекул (количество молекул в единице объема) диэлектрика. Для вектора электрического смещения имеем выражение:
\[\overrightarrow{D}={\varepsilon }_0\overrightarrow{E}+\overrightarrow{P}={\varepsilon }_0\overrightarrow{E}\left(1+n\beta \right)\left(3\right).\]Так как для изотропного диэлектрика имеет место уравнение:
\[\overrightarrow{D}=\varepsilon {\varepsilon }_0\overrightarrow{E}\left(4\right).\]Следовательно, получаем, что:
\[\varepsilon =1+n\beta \left(5\right).\]Уравнение (5) связывает диэлектрическую проницаемость $\varepsilon $ с концентрацией молекул в диэлектрике и поляризуемостью молекул. Формула (5) является приближенной, так как мы считали, что электрическое поле, которое вызывает смещение зарядов в молекуле, равно среднему полю в диэлектрике, что, в общем, неверно. Среднее поле ($\overrightarrow{E}$) учитывает действие всех зарядов, поле же $\overrightarrow{E'}$ - выражает действие всех зарядов за исключением рассматриваемой молекулы.
Напряженность локального поля
Для того, чтобы получить выражение диэлектрической проницаемости для плотных диэлектриков (жидкостей и твердых тел), необходимо найти напряженность локального поля $\overrightarrow{E'}$. Что является нетривиальной задачей, так как это поле существенно зависит от внутренней структуры диэлектрика. Для кристаллов с кубической решеткой по модели Лоренца в разделе «Локальное поле» нами было получено, что $\overrightarrow{E'}$ равно:
\[\overrightarrow{E'}=\overrightarrow{E}+\frac{\overrightarrow{P}}{3{\varepsilon }_0}\left(6\right),\]где $\overrightarrow{P}$ -- вектор поляризованности кристалла. Эту формулу приближенно можно применить к неполярным жидкостям и газам, в которых молекулы расположены хаотично.
Используя формулу (6) можно вычислить поляризованность плотных диэлектриков. В этом случае вектор поляризованности равен:
\[\overrightarrow{P}=n\beta {\varepsilon }_0\left(\overrightarrow{E}+\frac{\overrightarrow{P}}{3{\varepsilon }_0}\right)\left(7\right).\]Для вектора смещения, используя первую часть выражения (3) получаем равенство:
\[\overrightarrow{D}={\varepsilon }_0\overrightarrow{E}+\overrightarrow{P}={\varepsilon }_0\overrightarrow{E}+n\beta {\varepsilon }_0\left(\overrightarrow{E}+\frac{\overrightarrow{P}}{3{\varepsilon }_0}\right)={\varepsilon }_0\overrightarrow{E}+\frac{1}{3}n\beta \left(\overrightarrow{D}+2{\varepsilon }_0\overrightarrow{E}\right)\left(8\right).\]Формула Клаузиуса -- Моссотти
Так как для изотропного диэлектрика $\overrightarrow{D}=\varepsilon {\varepsilon }_0\overrightarrow{E},$ то из (8), следует, что:
\[\frac{\varepsilon -1}{\varepsilon +2}=\frac{n\beta }{3}\left(9\right).\]Формула (8), которая называется формулой Клаузиуса -- Моссотти, показывает, что для неполярных диэлектриков отношение, стоящее в левой части прямо пропорционально концентрации молекул, и, следовательно, плотности диэлектрика. Что хорошо подтверждается опытом. Помимо этого, если $n=const$, $\varepsilon $ не зависит от температуры, так как $\beta $ зависит только от строения молекулы. Этот факт, так же хорошо согласуется с опытом.
Задание: Оцените атомную диэлектрическую восприимчивость атома водорода ($\beta $). Считать, что напряженность внешнего поля направлена перпендикулярно плоскости движения электрона в атоме (рис.1).
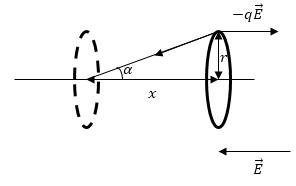
Рис. 1
Решение:
За основу решения задачи примем условие равновесия движущегося электрона во внешнем поле $\overrightarrow{E}:$
\[qE=\frac{q^2}{4\pi {\varepsilon }_0(x^2+r^2)}cos\alpha =\frac{q^2}{4\pi {\varepsilon }_0}\frac{x}{{(x^2+r^2)}^{{3}/{2}}}\ \left(1.1\right).\]Если принять, что $x\ll r$, то получим:
\[\frac{x}{{\left(x^2+r^2\right)}^{{3}/{2}}}\approx \frac{x}{r^3}\left(1.2\right).\]Значит, из (1.1) получим:
\[qE=\frac{q^2}{4\pi {\varepsilon }_0}\frac{x}{r^3}\to E=\frac{q}{4\pi {\varepsilon }_0}\frac{x}{r^3}\to qx=E4\pi {\varepsilon }_0r^3=p\ \left(1.3\right),\]где $p$=$\ qx$. Так как для неполярных диэлектриков мы имеем соотношение для дипольного момента молекулы вида:
\[\overrightarrow{p_e}=\beta {\varepsilon }_0\overrightarrow{E}\left(1.4\right),\]то используя (1.3) и (1.4) запишем для $\beta $:
\[\beta =4\pi r^3\ \left(1.5\right).\]Так в нормальном состоянии среднее расстояние электрона от ядра в атоме водорода составляет $r_H=0,53\cdot {10}^{-10}м$ (Боровский радиус) можно провести вычисления:
\[\beta =4\pi {\left(0,53\cdot {10}^{-10}\right)}^3\approx 1,87\cdot {10}^{-30}\left(м^3\right).\]Ответ: $\beta \approx 1,87\cdot {10}^{-30}м^3.$
Задание: Воздух в основном состоит из молекул азота и кислорода. Найдите приблизительно, средний радиус молекулы воздуха, если коэффициент атомной поляризуемости $\beta =1,1\cdot {10}^{-29}м^3$.
Решение:
За основу решения примем выражение, связывающее $\beta $ и радиус неполярной молекулы которое мы получили в предыдущем примере, а именно:
\[\beta =4\pi r^3\left(2.1\right).\]Выразим из него искомый радиус, получим:
\[r=\sqrt[3]{\frac{\beta }{4\pi }}\ \left(2.2\right).\]Проведем вычисления:
\[r=\sqrt[3]{\frac{1,1\cdot {10}^{-29}}{4\cdot 3,14}}\approx 0,96\cdot {10}^{-10}\left(м\right).\]Ответ: Радиус молекулы воздуха в среднем составляет $0,96\cdot {10}^{-10}м.$











