
Допустим, что объем диэлектрика постоянный, и он неподвижен. Такое предположение дает возможность не учитывать работу упругих и вязких сил при нахождении элементарной работы, которую производят внешние силы ($\delta A^{vnesh}$) при квазистатическом процессе электризации диэлектрика. В данном случае вся работа внешних сил идет на отделении положительного электричества от отрицательного и распределению заряда в пространстве.
Элементарное приращение электрической энергии
Если в изотропном диэлектрике взять две бесконечно малые плоские площадки, которые перпендикулярны вектору напряженности электрического поля $\overrightarrow{E}$. Расстояние между избранными площадками равно l и оно мало в сравнении с линейными размерами площадок. В таком случае площадки можно рассматривать как бесконечные плоскости, не учитывая краевые эффекты. Условимся, что внешние силы направлены против поля, и они переносят с одной площадки на другую заряд $\delta q=S\delta \sigma .$ Здесь $S$ -- площади плоскостей, $\delta \sigma $ -- приращение поверхностной плотности заряда на площадке, куда заряд перенесли. Работа внешних сил против поля в таком случае, равна:
где V - бесконечно маленький объем между площадками. Согласно теореме Остроградского -- Гаусса, электрическое поле изменяется только между площадками. Длина вектора электрического смещения изменяется на величину:
Получаем, что в изотропных средах сами векторы, а в неизотопных проекция вектора $\overrightarrow{D}\ $входят в выражение:
Надо обратить внимание, что объемы имелись в виду произвольной формы, переносимые заряды, также не обязательно одинаковы.
Мы считаем, что кроме работы по электризации диэлектрика, никакой работы над ним более не производится. При этом может выделяться тепло. Но мы пока его учитывать не будем. Тогда формула (3) определяет элементарное приращение электрической энергии в единицу объема пространства dw (плотность электрической энергии):
Соответственно, электрическая энергия равна:
В частности, если связь между вектором напряженности и вектором электрического смещения определена как:
где $\varepsilon =const$, то
Первое слагаемое выражения (7) совпадает с плотностью энергии поля в вакууме. Второе слагаемое, представляет собой энергию, которая тратится на поляризацию диэлектрика.
Полная электрическая энергия
Полная электрическая энергия (внутренняя или свободная) выражается формулой:
где интегрирование идет по всему пространству. Уравнение (8) представляет энергию в виде бесконечного множества слагаемых, каждое из которых равно $\frac{\varepsilon {\varepsilon }_0E^2dV}{2}$ и относится к определенному элементу объема $dV$.
Это означает, что носителем электрической энергии является электрическое поле, причем энергия локализована так, что в каждой единица объема содержится энергия $w$.
Задание: В однородное электростатическое поле с напряженностью $\overrightarrow{E_0}$ внесли диэлектрик с диэлектрической проницаемостью $\varepsilon .\ $Найдите энергию диэлектрика ($W_d$).
Решение:
Пусть электростатическое поле ($\overrightarrow{D_0}={\varepsilon }_0\overrightarrow{E_0}$) создается некоторым распределением зарядов в конечной области свободного пространства($\varepsilon =1$). Тогда энергия поля имеет вид:
\[W_0=\frac{1}{2}\int{\overrightarrow{E_0}\overrightarrow{D_0}}dV\ \left(1.1\right).\]Заполним пространство диэлектриком, но будем считать, что заряды не изменятся. Обозначим характеристики поля через $\overrightarrow{E}\ и\ \overrightarrow{D}={\varepsilon }_0\varepsilon \overrightarrow{E}$, где $\varepsilon $ -- диэлектрическая проницаемость среды. Полная энергия пространства после заполнения его диэлектриком равна:
\[W=\frac{1}{2}\int{\overrightarrow{E}}\overrightarrow{D}dV\ \left(1.2\right).\]Энергия диэлектрика ($W_d$), который помещен во внешнее поле с напряженностью $\overrightarrow{E_0}$, равна:
\[W_d=W-W_0=\frac{1}{2}\int{\left(\overrightarrow{E}\overrightarrow{D}-\overrightarrow{E_0}\overrightarrow{D_0}\right)}dV\ \left(1.3\right).\]Мы знаем, что при заполнении всего пространства однородным диэлектриком с проницаемостью $\varepsilon $ напряженность во всех точках поля уменьшается в $\varepsilon $ раз, то есть:
\[\overrightarrow{E}=\frac{\overrightarrow{E_0}}{\varepsilon }\ \left(1.4\right).\]Тогда имеем:
\[\overrightarrow{E}\overrightarrow{D}-\overrightarrow{E_0}\overrightarrow{D_0}=\overrightarrow{E}\varepsilon {\varepsilon }_0\overrightarrow{E}-е_0\overrightarrow{E_0}\cdot \overrightarrow{E_0}={\varepsilon }_0E^2_0\left(\frac{1}{\varepsilon }-1\right)=\left(1-\varepsilon \right)=-\frac{{\varepsilon }_0E^2_0}{\varepsilon }\varkappa =-\frac{1}{\varepsilon }{\overrightarrow{E}}_0\overrightarrow{P}\left(1.5\right).\] \[W_d=-\frac{1}{2\varepsilon }\int{\overrightarrow{E_0}\cdot \overrightarrow{P}}dV\ \left(1.6\right).\]Ответ: $W_d=-\frac{1}{2\varepsilon }\int{\overrightarrow{E_0}\cdot \overrightarrow{P}}dV.$
Задание: Найдите энергию, которая накоплена в двуслойном цилиндрическом конденсаторе длины l. Радиусы цилиндров $r_1$ и $r_2$, максимальный радиус первого диэлектрического слоя равен a (рис.1). Диэлектрические проницаемости цилиндров соответственно: ${\varepsilon }_1$ и ${\varepsilon }_2$. Обкладки конденсатора имеют заряд, равный по модулю $q.$
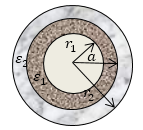
Рис. 1
Будем считать, что внутренней обкладке конденсатора находится заряд q, тогда для радиальной составляющей поле имеет вид:
\[E_r=\left\{ \begin{array}{c} \frac{1}{2\pi l{\varepsilon }_1}\frac{q}{r}\ при\ r_1 Энергию поля найдем по формуле: \[W=\frac{1}{2}\int{\overrightarrow{E}}\overrightarrow{D}dV\ \left(2.2\right).\]Подставим в (2.2) формулы из (2.1), получим:
\[W=\frac{1}{2}\int\limits^l_0{dl}\int\limits^a_{r_1}{{\left(\frac{q}{2\pi l}\right)}^2}\frac{1}{{\varepsilon }_1}\frac{1}{r^2}2\pi rdr+\frac{1}{2}\int\limits^l_0{dl}\int\limits^{r_2}_a{{\left(\frac{q}{2\pi l}\right)}^2}\frac{1}{{\varepsilon }_2}\frac{1}{r^2}2\pi rdr=\frac{q^2}{4\pi l}\left(\frac{1}{{\varepsilon }_1}ln\frac{a}{r_1}+\frac{1}{{\varepsilon }_2}ln\frac{r_2}{a}\right).\]Ответ: $W=\frac{q^2}{4\pi l}\left(\frac{1}{{\varepsilon }_1}ln\frac{a}{r_1}+\frac{1}{{\varepsilon }_2}ln\frac{r_2}{a}\right).$
















