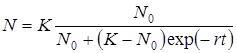Понятие поддерживающей емкости среды
Вместе с увеличением размеров и сложности системы увеличивается и функции системы и энергетическая стоимость поддержания структуры. При увеличении размеров системы в 2 раза более чем вдвое повышается число энергии, которая отводится на снижение энтропии.
В итоге, при росте сложности и размера системы показывается закон уменьшения отдачи, то есть повышаются затраты, которые связанны с масштабами, что можно объяснить ростом стоимости откачивания неупорядоченности. Но доля растущей платы за сложность покрывается преимуществами, называющимися экономией, которая связанна с масштабами.
Дополнительные функциональные петли и цепи обратной связи смогут усилить эффективность употребления энергии и вторичного употребления веществ и смогут увеличить устойчивость экосистемы к нарушающим влияниям. Поэтому с повышением величины и сложности системы имеет значение и закон увеличения отдачи.
Но, не смотря на преимущества от роста величин системы, суммарная энтропия очень быстро повышается с увеличением размеров. В итоге возрастает доля общего потока энергии, которая должна идти на дыхание, которое связанно с поддержанием системы, поэтому уменьшается доля энергии, идущая на новый рост.
В случае если затраты энергии на поддержание сравниваются с числом доступной энергии, рост системы кончается. число биомассы, которое поддерживаться в данных условиях, называют максимальной поддерживающей способностью (ёмкостью) среды. увеличение сложности и размеров популяций, в том числе и целых экосистем чаще всего протекает по S-образной кривой соответственно логистическому уравнению:
где К - наибольшая поддерживающая ёмкость среды, N0 – размер, который соответствует первоначальному моменту времени t = 0, r – удельная скорость роста.
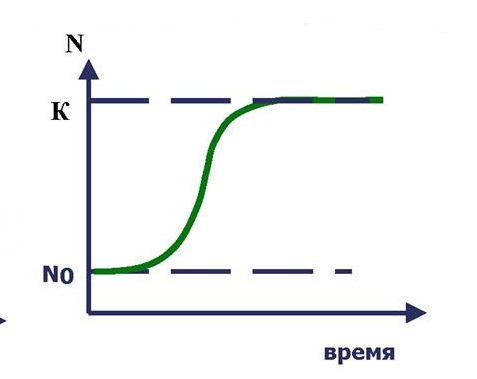
На данной кривой выделяют точку I или точку перегиба, где скорость роста наибольшая. величину I также называют оптимальной поддерживающей ёмкостью, потому что биомасса быстрее всего восстанавливаться на данном уровне.
На максимальном уровне К поддерживать систему весьма сложно, потому как из-за колебаний наружных условий габариты системы быть может превысят максимальную поддерживающую ёмкость среды и энтропия превзайдет способность системы рассеивать её. вследствие этого наилучшим было бы ограничить габариты системы на уровне оптимальной поддерживающей ёмкости среды, которая составляет 50% наибольшей, что разрешит устойчивое существование системе.
Поддерживающая емкость среды для города
Данный подход весьма актуален для населения Земли, потребление которого подступило к максимальной производительной способности планеты. всякое интенсивное стрессовое действие, например засуха, болезнь или война, сокращающие урожай даже на год, означает сильный голод или недоедание миллионов.
Проявление законов повышения и понижения отдачи при увеличении габаритов удобнее всего прослеживать на примере систем городов. С ростом размеров города идет концентрация больших производств, повышается заработная плата жителей большого города, в больших городах собираются спортивные культурные центры, образовательные и научные центры, что доставляет немало преимуществ обитателям больших городов. В больших городах постоянно имеется возможность удовлетворять почти любое требование человека. тем не менее вместе с увеличением площади города портится качество жизни за счет порчи качества воздуха и качества ОС. С ростом площади города повышаются:
- расходы на обслуживание и поддержание города;
- затраты на транспорт;
- безработица во время экономического спада;
- болезни населения;
- расходы на охлаждение и отопление;
- величина преступности.
Рациональный баланс между выгодами и затратами формируется в городах с умеренным размером жителей (100-200 тыс. человек).