
Свойства обратных тригонометрических функций
Для начала напомним свойства обратных тригонометрических функции, которые будут нам необходимы при решении уравнений и неравенств, содержащих обратные тригонометрические функции.
${arcsin \left(-x\right)\ }=-arcsinx$
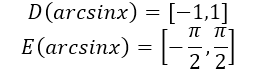
Рисунок 1.
${arccos \left(-x\right)\ }=\pi -arccosx$
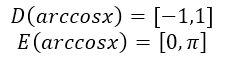
Рисунок 2.
${arctg \left(-x\right)\ }=-arctgx$
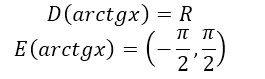
Рисунок 3.
${arcctg \left(-x\right)\ }=\pi -arcctgx$
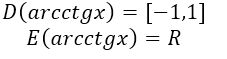
Рисунок 4.
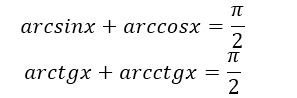
Рисунок 5.
Решение уравнений, содержащих обратные тригонометрические функции
- $arcsinf(x)=arcsing(x)\Leftrightarrow $
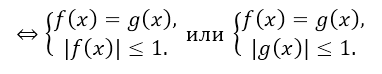
Рисунок 6.
- $arccosf(x)=arccosg(x)\Leftrightarrow $
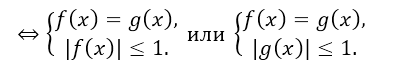
Рисунок 7.
-
$arctgf(x)=arctgg(x)\Leftrightarrow f\left(x\right)=g\left(x\right)$
-
$arcctgf(x)=arcctgg(x)\Leftrightarrow f\left(x\right)=g\left(x\right)$
-
$arctgf(x)=arcctgg(x)\Leftrightarrow f\left(x\right)g\left(x\right)=1$
-
$arcsinf(x)=arcctgg(x)\Leftrightarrow f^2\left(x\right)=\frac{1}{g^2\left(x\right)+1}$
-
$arccosf(x)=arctgg(x)\Leftrightarrow f^2\left(x\right)=\frac{1}{g^2\left(x\right)+1}$
-
$arcsinf(x)=arctgg(x)\Leftrightarrow f^2\left(x\right)=\frac{g^2\left(x\right)}{g^2\left(x\right)+1}$
-
$arccosf(x)=arcctgg(x)\Leftrightarrow f^2\left(x\right)=\frac{g^2\left(x\right)}{g^2\left(x\right)+1}$
Решение неравенств, содержащих обратные тригонометрические функции
- $arcsinf\left(x\right)
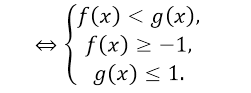
Рисунок 8.
- $arccosf\left(x\right)
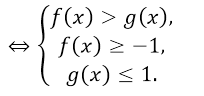
Рисунок 9.
$arctgf\left(x\right)
-
$arcctgf\left(x\right)g\left(x\right)$
Примеры задач на решение уравнений и неравенств, содержащих обратные тригонометрические функции
Решить уравнение ${arcsin \left(\frac{x}{4}\right)\ }=arcsin (x^2+\frac{x}{4}-9)$
Решение.
По формуле 1 получим, что данное уравнение равносильно следующей системе
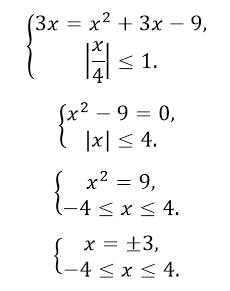
Рисунок 10.
Ответ: $\pm 3$.
Решить уравнение $3arctg\left(x-2\right)=1$
Решение.
\[arctg\left(x-2\right)=\frac{1}{3}\]$\frac{1}{3}$ можно записать в следующем виде: $\frac{1}{3}=arctg(tg\frac{1}{3})$
Получим: $arctg\left(x-2\right)=arctg(tg\frac{1}{3})$
По третьей формуле, получим:
\[x-2=tg\frac{1}{3}\] \[x=tg\frac{1}{3}+2\]Ответ: $tg\frac{1}{3}+2$.
Решить неравенство ${arccos \left(x^2-2x\right)\ }\le arccos (x)$
Решение.
По формуле 11, получим, что данное неравенство равносильно системе:
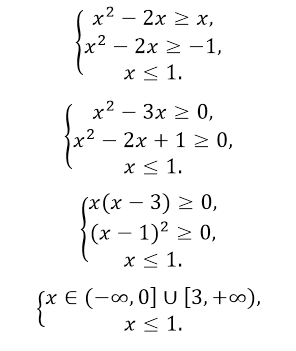
Рисунок 11.
Ответ: $\left(-\infty ,0\right].$
















