Определение смешанной дроби
В математике сумму $n+\frac{a}{b}$, где $n$ -натуральное число, $\frac{a}{b}$ -- правильная обыкновенная дробь, принято записывать без знака $«+»$ в виде $n\frac{a}{b}$.
Например, сумма $4+\frac{3}{5}$ записывается $4\frac{3}{5}$. Такая запись называется смешанной дробью, а число, которое ей соответствует, -- смешанным числом.
Смешанное число -- это число, которое равно сумме натурального числа $n$ и правильной обыкновенной дроби $\frac{a}{b}$, и записано в виде $n\frac{a}{b}$. В таком случае число $n$ называется $n\frac{a}{b}$, а число $\frac{a}{b}$ -- дробной частью числа/
Для смешанных чисел справедливы равенства $n\frac{a}{b}=n+\frac{a}{b}$ и $n+\frac{a}{b}=n\frac{a}{b}$.
Например, число $7\frac{4}{9}$ является смешанным числом, где натуральное число $7$ -- целая его часть, $\frac{4}{9}$ -- дробная часть. Примеры смешанных чисел: $17\frac{1}{2}$, $456\frac{111}{500}$, $23000\frac{4}{5}$.
Встречаются числа в смешанной записи, которые в дробной части содержат неправильную дробь. Например, $3\frac{54}{5}$, $56\frac{9}{2}$. Запись этих чисел можно представить в виде суммы их целой и дробной части. Например, $3\frac{54}{5}=3+\frac{54}{5}$ и $56\frac{9}{2}=56+\frac{9}{2}$. Такие числа не подходят по определению смешанного числа, т.к. дробная часть смешанных чисел должна быть правильной дробью.
Число $0\frac{2}{7}$ также не смешанное число, т.к. $0$ - не натуральное число.
Перевод смешанного числа в неправильную дробь
Алгоритм перевода смешанного числа в неправильную дробь:
-
Записать смешанное число $n\frac{a}{b}$ в виде суммы целой и дробной части этого числа, т.е. в виде $n+\frac{a}{b}$.
-
Целую часть исходного смешанного числа заменить дробью со знаменателем $1$.
-
Сложить обыкновенные дроби $\frac{n}{1}$ и $\frac{a}{b}$ для получения искомой неправильной дроби, равной исходному смешанному числу.
Представить смешанное число $7\frac{3}{5}$ в виде неправильной дроби.
Решение.
Воспользуемся алгоритмом перевода смешанного числа в неправильную дробь.
-
Смешанное число $7\frac{3}{5}=7+\frac{3}{5}$.
-
Запишем число $7$ в виде $\frac{7}{1}$.
-
Сложим обыкновенные дроби $\frac{7}{1}+\frac{3}{5}=\frac{35}{5}+\frac{3}{5}=\frac{38}{5}$.
Запишем краткую запись данного решения:
\[7\frac{3}{5}=7+\frac{3}{5}=\frac{7}{1}+\frac{3}{5}=\frac{35}{5}+\frac{3}{5}=\frac{38}{5}.\]Ответ: $7\frac{3}{5}=\frac{38}{5}$
Весь алгоритм перевода смешанного числа $n\frac{a}{b}$ в неправильную дробь сводится к \textit{формуле перевода смешанного числа в неправильную дробь}:
Записать смешанное число $14\frac{3}{5}$ в виде неправильной дроби.
Решение.
Воспользуемся формулой $n\frac{a}{b}=\frac{n\cdot b+a}{b}$ для перевода смешанного числа в неправильную дробь. В данном примере $n=14$, $a=3$, $b=5$.
Получим, $14\frac{3}{5}=\frac{14\cdot 5+3}{5}=\frac{73}{5}$.
Ответ: $14\frac{3}{5}=\frac{73}{5}$
Выделение целой части из неправильной дроби
При получении числового решения не принято оставлять ответ в виде неправильной дроби. Неправильная дробь преобразуется в равное ей натуральное число (если числитель делится нацело на знаменатель), или выделяют целую часть из неправильной дроби (если числитель не делится нацело на знаменатель).
Выделением целой части из неправильной дроби называется замена дроби равным ей смешанным числом.
Для выделения целой части из неправильной дроби нужно представить неправильную дробь $\frac{a}{b}$ в виде смешанного числа $q\frac{r}{b}$, где $q$ - неполное частное, $r$-- остаток от деления $a$ на $b$. Таким образом, целая часть равна неполному частному от деления $a$ на $b$, а остаток равен числителю дробной части.
Докажем это утверждение. Для этого достаточно показать, что $q\frac{r}{b}=\frac{a}{b}$.
Переведем смешанное число $q\frac{r}{b}$ в неправильную дробь с помощью формулы:
Т.к. $q$-- неполное частное, $r$-- остаток от деления $a$ на $b$, то является справедливым равенство $a=b\cdot q+r$. Таким образом, $\frac{q\cdot b+r}{b}=\frac{a}{b}$, откуда $q\frac{r}{b}=\frac{a}{b}$, что и требовалось показать.
Таким образом, сформулируем \textit{правило выделения целой части из неправильной дроби} $\frac{a}{b}$:
-
Разделить $a$ на $b$ с остатком, при этом определить неполное частное $q$ и остаток $r$.
-
Записать смешанное число $q\frac{r}{b}$, равное исходной дроби $\frac{a}{b}$.
Выделить целую часть из дроби $\frac{107}{4}$.
Решение.
Выполним деление в столбик:
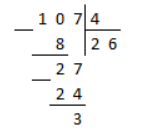
Рисунок 1.
Итак, в результате деления числителя $a=107$ на знаменатель $b=4$ получаем неполное частное $q=26$ и остаток $r=3$.
Получаем, что неправильная дробь $\frac{107}{4}$ равна смешанному числу $q\frac{r}{b}=26\frac{3}{4}$.
Ответ: $\frac{{\rm 107}}{{\rm 4}}{\rm =26}\frac{{\rm 3}}{{\rm 4}}$.
Сложение смешанного числа и натурального числа
Правило сложения смешанного и натурального числа:
Для сложения смешанного и натурального числа нужно к целой части смешанного числа прибавить данное натуральное число, дробная часть остается без изменения:
где $a\frac{b}{c}$ -- смешанное число,
$n$ -- натуральное число.
Выполнить сложение смешанного числа $23\frac{4}{7}$ и числа $3$.
Решение.
\[23\frac{4}{7}+3=\left(23+3\right)+\frac{4}{7}=26\frac{4}{7}.\]Ответ: $23\frac{4}{7}+3=26\frac{4}{7}.$
Сложение двух смешанных чисел
При сложении двух смешанных чисел складываются их целые части и дробные части.
Сложить смешанные числа $3\frac{1}{5}$ и $7\frac{4}{7}$.
Решение.
Воспользуемся формулой:
\[a\frac{b}{c}+d\frac{e}{f}=\left(a+d\right)+\left(\frac{b}{c}+\frac{e}{f}\right).\] \[3\frac{1}{5}+7\frac{4}{7}=\left(3+7\right)+\left(\frac{1}{5}+\frac{4}{7}\right)=10+\frac{1\cdot 7}{35}+\frac{4\cdot 5}{35}=10+\frac{27}{35}=10\frac{27}{35}.\]Ответ: $10\frac{27}{35}.$

















