Действительная функция $\xi =\varphi (\omega )$ определенная на измеримом пространстве $\{ \Omega ,{\rm F}\} $ называется измеримой или случайной величиной, если
\[\forall B\subset B(R):{\rm \; \; }\{ \omega :{\rm \; \; }\varphi (\omega )\subset B\} \subset {\rm F}\]или
прообраз $f^{-1} (B)={\rm \; }\{ \omega :{\rm \; \; }\varphi (\omega )\subset B\} $
является измеримым множеством в $\Omega$.
Вероятностная мера $P_{\xi } $ на $\{ R,B(R)\} $ с вероятностью $P_{\xi } =P\{ \omega :{\rm \; \; }\varphi (\omega )\subset B\} $, $B\subset B(R)$, называется распределением вероятностей случайной величины $\xi$ на измеримом пространстве $\{ R,B(R)\} $.
Функция
\[F_{\xi } (x)=P(\omega :{\rm \; }\varphi (\omega )это функция распределения случайной величины $\xi =\varphi (\omega )$.Дискретные случайные величины
Дискретной называется случайная величина, которая каждому элементарному событию $\omega$ ставит в соответствие одно из конечного или счетного набора
\[x_{1} ,x_{2} ,...,x_{n} , n\in N=\{ 1,2,3,...\} .\]Дискретная случайная величина полностью задается своим рядом распределения.
Пусть случайная величина $\xi$ принимает значения $x_{1}$

Рисунок 1. Таблица 1
или
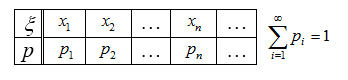
Рисунок 2. Таблица 2
Непрерывная случайная величина это функцию $\xi =\varphi (\omega )$, множеством значений которой является некоторый числовой интервал $(a,b)$, $a,b\in R$, $a
Функция $\rho _{\xi } (x)$ - это плотность распределения вероятностей (или плотностью распределения) непрерывной случайной величины $\xi$, если она удовлетворяет условиям:
-
$\forall x\in R$ $\rho _{\xi } (x)\ge 0$;
-
$\int \limits _{-\infty }^{\infty }\rho _{\xi } (x) dx=1$.
Легко показать, что
\[F_{\xi } (x)=\int \limits _{-\infty }^{x}\rho _{\xi } (t) dt. \]Случайная величина $\xi$ распределена по биномиальному закону, если ее значения являются количеством наступлений события $A$ в схеме Бернулли из $n$ испытаний, то есть, задается следующим рядом распределения (табл. 3)

Рисунок 3. Таблица 3
Общее число $\xi$ появлений события $A$ в $n$ испытаниях складывается из числа появлений события в отдельных независимых испытаниях $\xi _{i} $, $i=1,2,...,n$, где $\xi _{i} $ $-$ случайная величина, равная количеству наступлений события $A$ в $i$-ом испытании, то есть, распределение (табл. 4) каждой случайной величины $\xi _{i} $ имеет следующий вид:
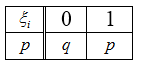
Рисунок 4. Таблица 4
Отсюда $M(\xi _{i} )=\sum \limits _{i=1}^{2}x_{i} \cdot p_{i} =0\cdot q+1\cdot p=p$;
\[D(\xi _{i} )=\sum \limits _{i=1}^{2}x_{i} ^{2} \cdot p_{i} -M^{2} (\xi _{i} )=0^{2} \cdot q+1^{2} \cdot p-p^{2} =p-p^{2} =\] \[=p\cdot (1-p)=p\cdot q.\]Воспользуемся свойствами математического ожидания и дисперсии, получим
В партии однотипных деталей стандартными являются $90\%$. Наугад берут 5 деталей. Найти закон распределения дискретной случайной величины $\xi $ - числа нестандартных деталей среди пяти тобраных. Определить $F(x)$.
Решение.
Целочисельная случайная величина $\xi $ имеет биномиальный закон расспределения вероятностей и может принимать значения $\xi $=0,1,3,3,4,5.
По условию задачи вероятность появления нестандартной детали $p=1-0$, $9=0,1$, а $q=0,9$ -- появление стандартной детали, $n=5$. Тогда $P_5\left(k\right)=$
\[C^k_5\cdot p^k\cdot q^{n-k}, k=0,1,2,3,4,5.\]В табличной форме закон расспределения случайной величины $\xi $ будет иметь вид:

Рисунок 5.
Проверим условие нормирования.
\[\sum\limits^5_{i=0}{p_i}=0,59049+0,32805+0,0729+0,0081+0,00045+0,00001.\]Условия нормирования выполняются, поэтому закон расспредиления вероятностей построено правельно.
Функция расспределения вероятностей выюора нестандартной детали из 5 произвольно взятых будет иметь вид
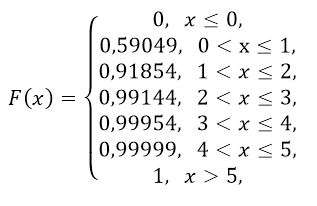
Рисунок 6.
Математическое ожидание этой случайной величины X, расспределенной по биномиальному закону равняется $M\left(x\right)=5\cdot 0,1=0,5$, а дисперсия $D\left(x\right)=5\cdot 0,1\cdot 0,9=0,45.$












