Понятие n-мерной случайной величины
Самый простой и дольно понятный случай -- это случай с использованием одной случайной величины $X$. Такая случайная величина называется одномерной случайной величиной. Помимо таких величин рассматриваются также величины, которые определяются двумя, тремя или $n$ значениями. Такие величины называются, соответственно, двумерными, трехмерными$, ... ,$ $n-$мерными случайными величинами. При этом каждое из значений называют составляющей случайной величины.
$n-$мерная случайная величина называется дискретной, если все её составляющие являются дискретными случайными величинами.
$n-$мерная случайная величина называется непрерывной, если все её составляющие являются непрерывными случайными величинами.
Понятие системы случайных величин
Составляющие $n-$мерной случайной величины, рассматриваемые вместе, называется системой $n$ случайных величин.
В дальнейшем, чаще всего, мы будем рассматривать систему двух случайных величин и обозначать её $(X,\ Y)$.
Случайная величина называется двумерной, если она определяется двумя числами.
Составляющие двумерной случайной величины, рассматриваемые вместе, называется системой двух случайных величин.
Законы распределения двумерной случайной величины
Законом распределения двумерной случайной величины $(X,Y)$ - называется множество возможных пар чисел $(x_i,\ y_j)$ (где $x_i \epsilon X,\ y_j \epsilon Y$) и их вероятностей $p_{ij}$.
Существуют три основных вида законов распределения случайной величины. Самый простой из них -- запись виде таблицы, где в первом столбце и строке значения случайных величин, а в остальных вероятности, связывающие их.
Ведем еще два вида законов распределения двумерной случайной величины.
Интегральной функцией распределения для двумерной случайной величины $(X,Y)$ называется функция $F\left(x,y\right)$ удовлетворяющая равенству
\[F\left(x,y\right)=P(XФункцией плотности распределения для двумерной случайной величины называется функция $\varphi (x,y)$, связанная с интегральной функцией распределения $F\left(x,y\right)$ соотношением
\[F\left(x,y\right)=\int\limits^x_{-\infty }{\int\limits^y_{-\infty }{\varphi \left(t,z\right)dtdz}}\]Вероятность попадания двумерной случайной величины в заданную область
Введем теперь две основные формулы для нахождения вероятности попадания двумерной случайной величины $(X,Y)$ в область $D$.
- Нахождение вероятности попадания двумерной случайной величины в заданную прямоугольную область с помощью интегральной функции распределения.
Причем, если $D$ -- прямоугольник, то
\[P\left(\left(X,Y\right)\in D\right)=\int\limits^{x_2}_{x_1}{\int\limits^{y_2}_{y_1}{\varphi \left(x,y\right)dxdy}}\]Примеры задач
Вероятность попадания в мишень при одном выстреле равняется $0,3$. Найти вероятность попадания такой случайной величины в прямоугольную область $ABCD$ с координатами вершин $A(0,0)$, $B=(0,2)$, $C=\left(1,2\right),\ D(1,0)$.
Решение.
Составим сначала закон распределения данной случайной величины. Пусть $X$ число попаданий в мишень, а $Y$ - число промахов в мишень. Вероятность промаха равна $1-0,3=0,7$. Из этого всего получаем следующий закон распределения случайной величины $(X,Y)$:

Рисунок 1.
Из полученного закона, очевидно, что функция распределения имеет вид:
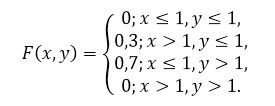
Рисунок 2.
Так как $D$ - прямоугольник, то для нахождения вероятности попадания случайной величины в этот прямоугольник будем искать по формуле
\[P\left(x_1Получим: \[P\left(0Ответ: 0,4.Распределение двумерной случайной величины задано функцией плотности распределения, имеющей вид
\[\varphi \left(x,y\right)=\frac{2}{{\pi }^2\left(4+x^2\right)(1+y^2)}\]Найти вероятность попадания такой случайной величины область $D$, ограниченную прямыми $x=0,\ x=2,\ y=0,\ y=1$.
Решение:
Так как нам задана плотность распределения двумерной случайной величины и область $D$ -- прямоугольник, то воспользуемся следующей формулой для вычисления вероятности попадания данной величины в область $D$
\[P\left(\left(X,Y\right)\in D\right)=\int\limits^{x_2}_{x_1}{\int\limits^{y_2}_{y_1}{\varphi \left(x,y\right)dxdy}}\] \[P\left(\left(X,Y\right)\in D\right)=\int\limits^2_0{\int\limits^1_0{\frac{2}{{\pi }^2\left(4+x^2\right)(1+y^2)}dxdy}}=\frac{2}{{\pi }^2}\int\limits^2_0{\int\limits^1_0{\frac{dxdy}{\left(4+x^2\right)(1+y^2)}}}=\] \[=\frac{2}{{\pi }^2}\int\limits^2_0{\frac{dx}{4+x^2}}\int\limits^1_0{\frac{dy}{1+y^2}}=\frac{2}{{\pi }^2}\int\limits^2_0{\frac{dx}{4+x^2}}\cdot {\left.\left(arctgy\right)\right|}^1_0=\] \[=\frac{2}{{\pi }^2}\left(\frac{\pi }{4}+0\right)\int\limits^2_0{\frac{dx}{4+x^2}}=\frac{1}{2\pi }{\left.\left(\frac{1}{2}arctg\frac{x}{2}\right)\right|}^2_0=\frac{1}{4\pi }\left(\frac{\pi }{4}+0\right)=\frac{1}{16}\] \[P\left(\left(X,Y\right)\in D\right)=0,0625\]Ответ: $0,0625$.











