Таблица производных

Источник статьи

Автор24 — учеба по твоим правилам

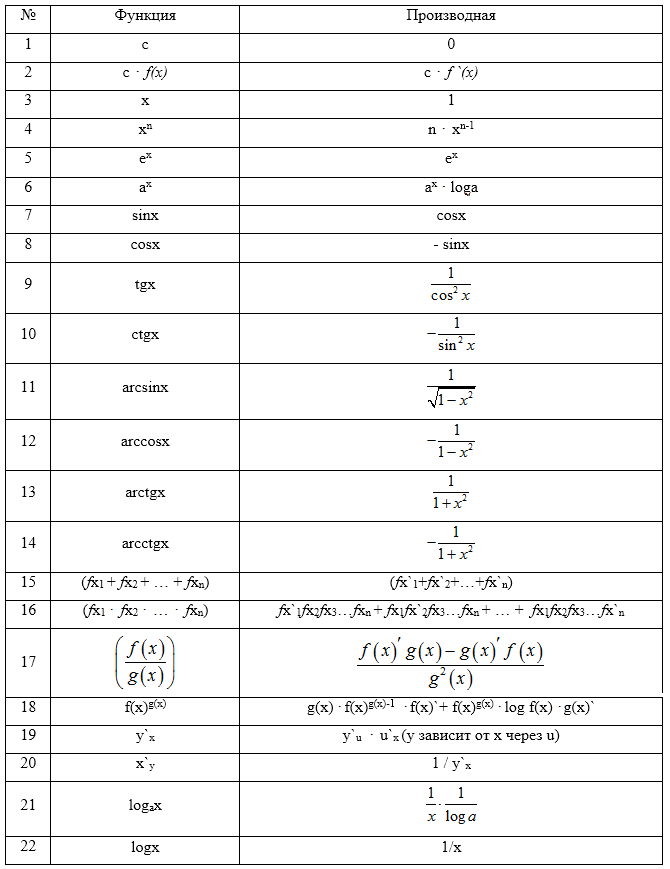
Приведем таблицу производных элементарных функций

Таблица 1

Производные функций

Пример 1

Вычислить по таблице производную функции

$y=2x^{3} -2x^{2} +4x-1$

Решение.

$y`=2\cdot 3x^{2} -2\cdot x^{1} +4=6x^{2} -2x+4$

Применили свойства 2 и 4 таблицы 1.

Пример 2

Вычислить по таблице производную функции

$y=\frac{1}{\sqrt[{3}]{x^{2} } }$

Решение.

$y`=\left(x^{-\frac{2}{3} } \right)^{{'} } =-\frac{2}{3} x^{-\frac{2}{3} -1} =-\frac{2}{3} x^{-\frac{2}{3} -\frac{3}{3} } =-\frac{2}{3} x^{-\frac{5}{3} } =-\frac{2}{3x\sqrt[{3}]{x^{2} } }$

Применили свойство 4 таблицы 1.

Пример 3

Вычислить по таблице производную функции

$y=\sin ^{2} x$

Решение.

$y`=2f(x)*f(x)=2\sin x\cos x=\sin 2x$

Применили свойство 4, 7, 19 таблицы 1.

Пример 4

Вычислить по таблице производную функции

$y=\sin x^{2}$

Решение.

$y`=\cos (\sin x)sin'x=2x\cos x^{2}$

Применили свойство 4, 7, 19 таблицы 1.

Пример 5

Вычислить по таблице производную функции

$y=\log (x+\sqrt{x^{2} +1} )$

Решение.

Полагая, в первом случае, что u = $x+\sqrt{x^{2} +1}$ , а во втором, что u = х2 + 1, дважды применим свойство 19, а затем 21, 15, 4.

$y`=\frac{1}{x+\sqrt{x^{2} +1} } \left(x+\sqrt{x^{2} +1} \right)^{{'} } =\frac{1}{x+\sqrt{x^{2} +1} } \left[1+\left(\sqrt{x^{2} +1} \right)^{{'} } \right]=$

$=\frac{1}{x+\sqrt{x^{2} +1} } \left[1+\frac{1}{2\sqrt{x^{2} +1} } \left(x^{2} +1\right)^{{'} } \right]=\frac{1}{x+\sqrt{x^{2} +1} } \left(1+\frac{x}{\sqrt{x^{2} +1} } \right)=$