Что такое касательная и нормаль к кривой
Касательная -- прямая которая совпадает и проходит через точку кривой с точностью до первого порядка.
Нормаль к кривой -- прямая перпендикулярно проходящая через точку касания.
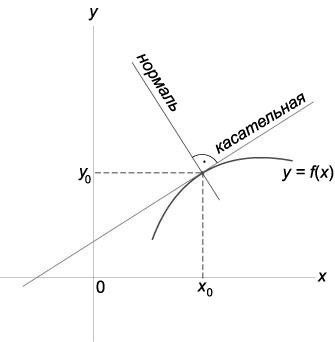
Рисунок 1. Нормаль и касательная к кривой
Для кривой вида y = f(x) уравнение касательной в точке М(x0,y0):
\[y-y_{0} =y`(x_{0} )(x-x_{0} )\]Для кривой вида y = f(x) уравнение касательной в точке М(x0,y0):
\[y-y_{0} =-\frac{1}{y`(x_{0} )} (x-x_{0} )\]Написать уравнение касательной и нормали к кривой в точке с абсциссой $x_0=1$:
\[y=3x^{2} -2x+11\]Решение.
- Найдем значение функции в точке: \[y_{0} =3\cdot 1^{2} -2\cdot 1+11=12\]
- Найдем производную в данной точке: \[y'(x_{0} )=\left(3x^{2} -2x+11\right){{'} } =6x-2\] \[y'(1)=6\cdot 1-2=4\]
- Запишем уравнение касательной: \[y-y_{0} =y`(x_{0} )(x-x_{0} )\] \[y-12=4(x-1)\] \[y-4x-8=0\]
- Запишем уравнение нормали: \[y-12=-\frac{1}{4} (x-1)\] \[4y+x-49=0\]
Угол между двумя кривыми в точке М(x0,y0) является наименьшим из возможных углов между касательными. Пусть уравнения касательных имеют вид:
$y=f_{1} (x)$ и $y=f_{2} (x)$
$y=k_{1} x+b_{1} $ и $y=k_{2} x+b_{2} $
Тогда тангенс угла между двумя кривыми находится по формуле:
\[tg\gamma =\frac{k_{2} -k_{1} }{1+k_{1} k_{2} } =\frac{f'_{2} (x_{0} )-f'_{1} (x_{0} )}{1+f'_{1} (x_{0} )f'_{2} (x_{0} )} \]Найти тангенс угла между кривыми, в точке имеющей большую абсциссу.
\[\begin{array}{l} {y=2x^{2} -3} \\ {y=4x-2} \end{array}\]Решение.
- Для того чтобы определить точки пересечения кривых необходимо решить систему уравнений: \[\left\{\begin{array}{l} {y=2x^{2} -3} \\ {y=4x-2} \end{array}\right. \] \[2x^{2} -3=4x-2\] \[2x^{2} -4x=1\] \[2x(x-2)=1\]
- Найдем производные в найденной точке \[y_{1} {{'} } =\left(2x^{2} -3\right){{'} } =4x\] \[y_{2} {{'} } =\left(4x-2\right){{'} } =4\] \[y_{1} {{'} } =4\cdot 2=8\] \[y_{2} {{'} } =4\]
- Запишем уравнение тангенса угла и подставим все известные значения \[tg\gamma =\frac{4-8}{1+8\cdot 4} =\frac{-4}{33} \]
Значит, кривые пересекаются в точках 0,5 и 2. Максимальной, из которых, является точка x = 2.
Длина отрезка от пересечения касательной оси ОХ до пересечения с нормалью или кривой называется длиной касательной.
Проекция отрезка от пересечения касательной оси ОХ до пересечения с нормалью или кривой на ось Ох называется подкасательной (ST).
Длина отрезка от пересечения нормали с касательной или кривой до точки соприкосновения с осью Ох называется длиной нормали, а проекция отрезка на ось -- поднормалью (SN).
Найти длину подкасательной и поднормали для эллипса x = acost, y = bsint
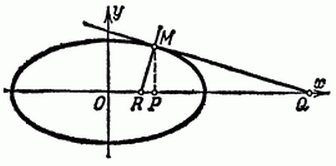
Рисунок 2. Эллипс
Решение.
- Уравнение касательной имеет вид: \[y-\frac{b}{\sqrt{2} } =-\frac{b}{a} (x-\frac{a}{\sqrt{2} } )\]
- Уравнение нормали имеет вид: \[y-\frac{b}{\sqrt{2} } =\frac{a}{b} (x-\frac{a}{\sqrt{2} } )\]
- Длины подкасательной и поднормали: \[S_{T} =\left|\frac{\frac{b}{\sqrt{2} } }{-\frac{b}{a} } \right|=\frac{a}{\sqrt{2} } \] \[S_{N} =\left|\frac{b}{\sqrt{2} } \left(-\frac{b}{a} \right)\right|=\frac{b^{2} }{a\sqrt{2} } \]












