Найти координаты центра тяжести (КЦТ) материальной плоской фигуры в виде криволинейной трапеции (КрТ), образованной кривой $y=\frac{150}{12\cdot x+3} $ между точками с абсциссами $x=1$ и $x=6$. Поверхностную плотность фигуры считать величиной постоянной. Выполнить графические построения.
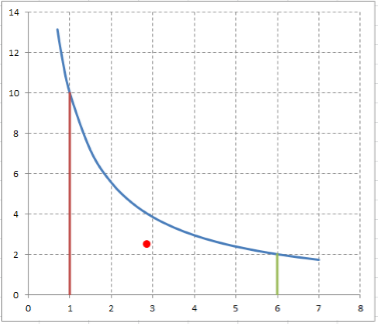
График данной криволинейной трапеции:
КЦТ материальной плоской фигуры в виде КрТ, образованной кривой $y=y\left(x\right)$ на промежутке $\left[a,\; b\right]$, вычисляют по формулам $x_{C} =\frac{\int \limits _{a}^{b}x\cdot y\left(x\right)\cdot dx }{\int \limits _{a}^{b}y\left(x\right)\cdot dx } $ и $y_{C} =\frac{\frac{1}{2} \cdot \int \limits _{a}^{b}y^{2} \left(x\right)\cdot dx }{\int \limits _{a}^{b}y\left(x\right)\cdot dx } $.
Находим интеграл $I_{1} =\int \limits _{a}^{b}y\left(x\right)\cdot dx $:
\[I_{1} =\int \limits _{1}^{6}\frac{150}{12\cdot x+3} \cdot dx =\frac{150}{12} \cdot \left[\ln \left|12\cdot x+3\right|\right]_{1}^{6} =\] \[=\frac{150}{12} \cdot \left(\ln \left|12\cdot 6+3\right|-\ln \left|12\cdot 1+3\right|\right)=\] \[=12,5\cdot \left(\ln 75-\ln 15\right)=12,5\cdot \ln \frac{75}{15} =12,5\cdot \ln 5\approx 12,5\cdot 1,609\approx 20,11; \]Находим интеграл $I_{2} =\frac{1}{2} \cdot \int \limits _{a}^{b}y^{2} \left(x\right)\cdot dx $:
\[I_{2} =\frac{1}{2} \cdot \int \limits _{1}^{6}\frac{150^{2} }{\left(12\cdot x+3\right)^{2} } \cdot dx =\frac{150^{2} }{2} \cdot \int \limits _{1}^{6}\left(12\cdot x+3\right)^{-2} \cdot dx =\] \[=\frac{150^{2} }{2\cdot 12} \cdot \left[\frac{\left(12\cdot x+3\right)^{-2+1} }{-2+1} \right]_{1}^{6} =-\frac{150^{2} }{24} \cdot \left[\frac{1}{12\cdot x+3} \right]_{1}^{6} =\] \[=-\frac{150^{2} }{24} \cdot \left(\frac{1}{12\cdot 6+3} -\frac{1}{12\cdot 1+3} \right)=-\frac{150^{2} }{24} \cdot \left(\frac{1}{75} -\frac{1}{15} \right)=\] \[=-\frac{150^{2} }{24} \cdot \frac{1-5}{75} =\frac{150^{2} }{24} \cdot \frac{4}{75} =\frac{150^{2} }{6\cdot 75} =50.\]Находим интеграл $I_{3} =\int \limits _{a}^{b}x\cdot y\left(x\right)\cdot dx $:
\[I_{3} =\int \limits _{1}^{6}x\cdot \frac{150}{12\cdot x+3} \cdot dx =\int \limits _{1}^{6}\frac{150\cdot x}{12\cdot x+3} \cdot dx =\] \[=\int \limits _{1}^{6}\frac{12\cdot 150\cdot x}{12\cdot \left(12\cdot x+3\right)} \cdot dx =\int \limits _{1}^{6}\frac{12\cdot 150\cdot x+150\cdot 3-150\cdot 3}{12\cdot \left(12\cdot x+3\right)} \cdot dx =\] \[=\int \limits _{1}^{6}\frac{150\cdot \left(12\cdot x+3\right)-150\cdot 3}{12\cdot \left(12\cdot x+3\right)} \cdot dx =\int \limits _{1}^{6}\frac{150\cdot \left(12\cdot x+3\right)}{12\cdot \left(12\cdot x+3\right)} \cdot dx -\] \[-\int \limits _{1}^{6}\frac{150\cdot 3}{12\cdot \left(12\cdot x+3\right)} \cdot dx =\frac{150}{12} \cdot \int \limits _{1}^{6}dx -\frac{3}{12} \cdot \int \limits _{1}^{6}\frac{150}{12\cdot x+3} \cdot dx =\] \[=\frac{150}{12} \cdot \left[x\right]_{1}^{6} -\frac{3}{12} \cdot I_{1} \approx 12,5\cdot \left(6-1\right)-\frac{3}{12} \cdot 20,11\approx 62,5-5,03\approx 57,47.\]Вычисляем КЦТ:
\[x_{C} =\frac{\int \limits _{a}^{b}x\cdot y\left(x\right)\cdot dx }{\int \limits _{a}^{b}y\left(x\right)\cdot dx } =\frac{I_{3} }{I_{1} } \approx \frac{57,47}{20,11} \approx 2,86;\] \[y_{C} =\frac{\frac{1}{2} \cdot \int \limits _{a}^{b}y^{2} \left(x\right)\cdot dx }{\int \limits _{a}^{b}y\left(x\right)\cdot dx } =\frac{I_{2} }{I_{1} } \approx \frac{50}{20,11} \approx 2,49.\]Центр тяжести отмечен на рисунке красной точкой.
Найти КЦТ материальной кривой в виде ломаной линии, проходящей последовательно через заданные точки $M\left(1,\; 4\right)$,~$N\left(3,\; 2\right)$ и $K\left(8,\; 3\right)$. Линейную плотность ломаной считать величиной постоянной. Выполнить графические построения.
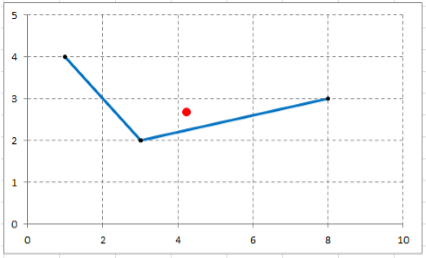
График данной ломаной:
Формулы для вычисления КЦТ плоской кривой имеют вид $x_{C} =\frac{\int \limits _{a}^{b}x\cdot \sqrt{1+y'^{2} \left(x\right)} \cdot dx }{\int \limits _{a}^{b}\sqrt{1+y'^{2} \left(x\right)} \cdot dx } $ и $y_{C} =\frac{\int \limits _{a}^{b}y\left(x\right)\cdot \sqrt{1+y'^{2} \left(x\right)} \cdot dx }{\int \limits _{a}^{b}\sqrt{1+y'^{2} \left(x\right)} \cdot dx } $.
Находим уравнения прямых, учитывая, что общее уравнение прямой имеет следующий вид:
$A\cdot x+B\cdot y+C=0$, где $A=y_{2} -y_{1} $, $B=x_{1} -x_{2} $, $C=-A\cdot x_{1} -B\cdot y_{1} $.
- Для прямой $MN$ имеем такие значения коэффициентов: \[A=y_{2} -y_{1} =2-4=-2; B=x_{1} -x_{2} =1-3=-2;\] \[C=-A\cdot x_{1} -B\cdot y_{1} =2\cdot 1+2\cdot 4=10.\]
- Для прямой $NK$ имеем такие значения коэффициентов: \[A=y_{2} -y_{1} =3-2=1; B=x_{1} -x_{2} =3-8=-5; \] \[C=-A\cdot x_{1} -B\cdot y_{1} =-1\cdot 3+5\cdot 2=7.\]
Уравнение прямой $MN$: $-2\cdot x-2\cdot y+10=0$ или $-x-y+5=0$.
Уравнение прямой $NK$: $x-5\cdot y+7=0$.
Находим выражение $\sqrt{1+y'^{2} } $ для данных прямых:
- для прямой $MN$ $y=-x+5$, $y'=-1$, $\sqrt{1+y'^{2} } =\sqrt{2} \approx 1,41$.
- для прямой $NK$ $y=\frac{1}{5} \cdot x+\frac{7}{5} $, $y'=\frac{1}{5} $, $\sqrt{1+y'^{2} } =\frac{\sqrt{26} }{5} \approx 1,02$.
Находим интеграл $I_{1} =\int \limits _{a}^{b}x\cdot \sqrt{1+y'^{2} } \cdot dx $ вдоль всей ломаной:
\[I_{1} =1,41\cdot \int \limits _{1}^{3}x\cdot dx +1,02\cdot \int \limits _{3}^{8}x\cdot dx =1,41\cdot \left[\frac{x^{2} }{2} \right]_{1}^{3} +1,02\cdot \left[\frac{x^{2} }{2} \right]_{3}^{8} =\] \[=\frac{1,41}{2} \cdot \left(3^{2} -1^{2} \right)+\frac{1,02}{2} \cdot \left(8^{2} -3^{2} \right)=\frac{1,41}{2} \cdot 8+\frac{1,02}{2} \cdot 55\approx 33,69.\]Находим интеграл $I_{2} =\int \limits _{a}^{b}y\cdot \sqrt{1+y'^{2} } \cdot dx $ вдоль всей ломаной:
\[I_{2} =1,41\cdot \int \limits _{1}^{3}\left(-x+5\right)\cdot dx +1,02\cdot \int \limits _{3}^{8}\left(\frac{1}{5} \cdot x+\frac{7}{5} \right)\cdot dx =\] \[=1,41\cdot \left[-\frac{x^{2} }{2} +5\cdot x\right]_{1}^{3} +1,02\cdot \left[\frac{1}{5} \cdot \frac{x^{2} }{2} +\frac{7}{5} \cdot x\right]_{3}^{8} =1,41\cdot 6+1,02\cdot \frac{125}{10} \approx 21,21.\]Находим интеграл $I_{3} =\int \limits _{a}^{b}\sqrt{1+y'^{2} } \cdot dx $ вдоль всей ломаной:
\[I_{3} =1,41\cdot \int \limits _{1}^{3}dx +1,02\cdot \int \limits _{3}^{8}dx =1,41\cdot 2+1,02\cdot 5\approx 7,92.\]Находим КЦТ ломаной линии:
\[x_{C} =\frac{\int \limits _{a}^{b}x\cdot \sqrt{1+y'^{2} \left(x\right)} \cdot dx }{\int \limits _{a}^{b}\sqrt{1+y'^{2} \left(x\right)} \cdot dx } =\frac{I_{1} }{I_{3} } \approx \frac{33,69}{7,92} \approx 4,25; \] \[y_{C} =\frac{\int \limits _{a}^{b}y\left(x\right)\cdot \sqrt{1+y'^{2} \left(x\right)} \cdot dx }{\int \limits _{a}^{b}\sqrt{1+y'^{2} \left(x\right)} \cdot dx } =\frac{I_{2} }{I_{3} } \approx \frac{21,21}{7,92} \approx 2,68.\]Центр тяжести отмечен на рисунке красной точкой.












