Замечательные пределы носят название «замечательных» благодаря своему свойству упрощать нахождение сложных пределов.
Первый замечательный предел
\[\mathop{\lim }\limits_{x\to 0} \frac{\sin x}{x} =1\](для натуральных значений х)
Доказательство
Первый замечательный предел">
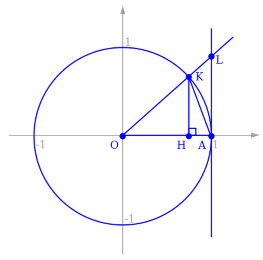
- Пусть х лежит в области (0; $\pi $/2). На единичной окружности данная область ограничена прямыми ОК и О1.
- Точка пересечения луча и окружности -- К, касательная к окружности -- L, а проекция К на ОХ обозначена точкой H.
- Из рисунка видно, что \[S_{\Delta OKA} где $S_sOKA$ -- площадь сектора ОКА \[S_{\Delta OKA} =\frac{1}{2} \left|OA\right|\left|KH\right|=\frac{1}{2} \cdot 1\cdot 1\cdot \sin x=\frac{\sin x}{2} \] \[S_{sOKA} =\frac{1}{2} R^{2} x=\frac{x}{2} \] \[S_{\Delta OAL} =\frac{1}{2} \left|OA\right|\left|LA\right|=\frac{tgx}{2} \]
- Подставим полученные выражения в неравенство \[\frac{\sin x}{2} Поскольку х стремится к 0: \[\frac{1}{tgx}
Следствия первого замечательного предела
- $\mathop{\lim }\limits_{x\to 0} \frac{tgx}{x} =1$
- $\mathop{\lim }\limits_{x\to 0} \frac{\arcsin x}{x} =1$
- $\mathop{\lim }\limits_{x\to 0} \frac{arctgx}{x} =1$
- $\mathop{\lim }\limits_{x\to 0} \frac{1-\cos x}{\frac{x^{2} }{2} } =1$
Пример 1
Вычислить предел
\[\mathop{\lim }\limits_{x\to 0} \frac{x}{\arcsin x} \]Решение: Используем метод замены переменной
\[\mathop{\lim }\limits_{x\to 0} \frac{x}{\arcsin x} =\left[\begin{array}{c} {y=\arcsin x\to x=\sin y} \\ {x\to 0;y\to 0} \end{array}\right]=\mathop{\lim }\limits_{y\to 0} \frac{\sin y}{y} =\frac{1}{1} =1\]Пример 2
Вычислить предел
\[\mathop{\lim }\limits_{x\to 0} \frac{\sin 7x}{3x} \]Решение: Подведем знаменатель под аргумент числителя
\[\mathop{\lim }\limits_{x\to 0} \frac{\sin 7x}{3x} =\frac{\sin 7x}{3\cdot \frac{1}{7} \cdot 7x} =\frac{1}{3\cdot \frac{1}{7} } =\frac{7}{3} \]Пример 3
Вычислить предел
\[\mathop{\lim }\limits_{x\to 0} \frac{1-\cos 2x}{xtgx} \]Решение: Применим законы тригонометрических преобразований
\[\mathop{\lim }\limits_{x\to 0} \frac{1-\cos 2x}{xtgx} =\mathop{\lim }\limits_{x\to 0} \frac{1-(\cos ^{2} x-\sin ^{2} x)}{xtgx} =\mathop{\lim }\limits_{x\to 0} \frac{\cos ^{2} x+\sin ^{2} x-\cos ^{2} x+\sin ^{2} x}{xtgx} =\] \[=\mathop{\lim }\limits_{x\to 0} \frac{2\sin ^{2} x}{xtgx} =\frac{2\sin x\cos x}{x\frac{\sin x}{\cos x} } =2\mathop{\lim }\limits_{x\to 0} \frac{\sin x}{x} \mathop{\lim }\limits_{x\to 0} \cos x=\left[2\cdot 1\cdot 1\right]=2\]Второй замечательный предел
\[\mathop{\lim }\limits_{x\to \infty } \left(1+\frac{1}{x} \right)^{x} =\mathop{\lim }\limits_{x\to 0} \left(1+x\right)^{1/x} =e\](для вещественных значений х)
Доказательство
- Если х стремится к бесконечности, каждое значение х располагается между положительными целыми. Где n -- целая часть числа х. \[ n\le x Таким образом, \[\frac{1}{n+1} Если х стремится к бесконечности, то и n так же стремится к $\infty $. \[\mathop{\lim }\limits_{n\to \infty } \left(1+\frac{1}{n+1} \right)^{n} =\frac{\mathop{\lim }\limits_{n\to \infty } \left(1+\frac{1}{n+1} \right)^{n+1} }{\mathop{\lim }\limits_{n\to \infty } \left(1+\frac{1}{n+1} \right)} =\frac{e}{1} =e\] \[\mathop{\lim }\limits_{n\to \infty } \left(1+\frac{1}{n} \right)^{n+1} =\mathop{\lim }\limits_{n\to \infty } \left(1+\frac{1}{n} \right)^{n} \cdot \mathop{\lim }\limits_{n\to \infty } \left(1+\frac{1}{n} \right)=e\cdot 1=e\]
- По признаку о пределе промежуточной функции: \[\mathop{\lim }\limits_{x\to \infty } \left(1+\frac{1}{x} \right)^{x} =e\]
Следствия второго замечательного предела
- $\mathop{\lim }\limits_{x\to 0} \left(1+x\right)^{\frac{1}{x} } =e$
- $\mathop{\lim }\limits_{x\to \infty } \left(1+\frac{k}{x} \right)^{x} =e^{k} $
- $\mathop{\lim }\limits_{x\to 0} \frac{\ln \left(1+x\right)}{x} =1$
- $\mathop{\lim }\limits_{x\to 0} \frac{e^{x} -1}{x} =1$
- $\mathop{\lim }\limits_{x\to 0} \frac{a^{x} -1}{x\ln a} =1\begin{array}{cc} {} & {} \end{array}(a>0,a\ne 1)$
- $\mathop{\lim }\limits_{x\to 0} \frac{\left(1+x\right)^{a} -1}{ax} =1$
Пример 4
Вычислить предел
\[\mathop{\lim }\limits_{x\to \infty } (1+\frac{1}{n} )^{n+5} \]Решение:
\[\mathop{\lim }\limits_{x\to \infty } (1+\frac{1}{n} )^{n+5} =\mathop{\lim }\limits_{x\to \infty } (1+\frac{1}{n} )^{n} \cdot (1+\frac{1}{n} )^{5} =e\mathop{\lim }\limits_{x\to \infty } (1+\frac{1}{n} )^{5} =e\cdot 1=e\]Пример 5
Вычислить предел
\[\mathop{\lim }\limits_{x\to 0} (1+x)^{\frac{3}{x} } \]Решение:
\[\mathop{\lim }\limits_{x\to 0} (1+x)^{\frac{3}{x} } =\mathop{\lim }\limits_{x\to 0} \left((1+x)^{\frac{1}{x} } \right)^{3} =e^{3} \]
Дата последнего обновления статьи: 17.12.2024
