Локальная теорема Лапласа
Пусть проводится $n$ испытаний Бернулли с вероятностью р появления события А в каждом из них. Пусть при этом $n$ достаточно большое число и $npq$ ≥ 10 ($n$ -- большое, а $p$ -- не очень маленькое) Тогда вероятность, того, что событие А произойдет ровно k раз может быть найдена по приближенной формуле:
таблица значений функции $\varphi$$(x)$обычно приводится в задачниках Теории вероятностей.
Свойства функции $\varphi$$\left(x\right):$
- $\varphi$$\left(x\right)>0$
- $\varphi$$\left(-x\right)=$$\varphi$$\left(x\right)$
- ${\mathop{lim}_{n\to \infty } (x)\ }=0,\ \ \ (\left(x\right)
Какова вероятность, что из 100 новорожденных ровно 40 окажутся мальчики.
\[\left. \begin{array}{c} n=100 \\ k=40 \\ p=0,5 \end{array} \right\} x=\frac{k-np}{\sqrt{npq}}=\frac{40-100\cdot 0,5}{\sqrt{100\cdot 40\cdot 0,5}}=-2\] \[P_{100}\left(40\right)=\frac{1}{\sqrt{100\cdot 0,5\cdot 0,5}}\varphi \left(-2\right)=\frac{1}{5}\varphi \left(-2\right)=\frac{1}{5}\varphi \left(2\right)=\frac{1}{5}\cdot 0,054=0,04\]Интегральная теорема Лапласа
В условиях локальной теоремы Лапласа вероятность того, что событие А произойдет от $k_1$ до $k_2$ раз $\left(k_1\le k\le k_2\right)$
\[P_n\left(k_1;k_2\right)=\left(x"\right)-\left(x'\right)\] \[x"=\frac{k_2-np}{\sqrt{npq}}\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ x'=\frac{k_1-np}{\sqrt{npq}}\]$P\left(x\right)=\frac{1}{\sqrt{2\pi }}\int{e^{\frac{-t^2}{2}dt}}-$формула Лапласа
Иногда функцией Лапласа называется выражение несколько отличающееся от написанного.
Свойство функции Лапласа:
- $\left(-x\right)=\left(x\right)$
- $\left(x\right)$ -- монотонно возрастает
- $0,5
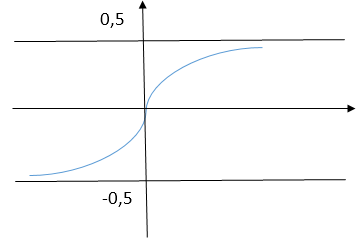Локальная и интегральная теоремы Лапласа">
Замечание: функция Лапласа $\left(x\right)$ связана с $\left(x\right):\ \ \ \left(x\right)=\int\nolimits^x_0{\left(t\right)dt}$
Схожесть семян составляет 90%. Какова вероятность, что из 100 семян взойдут от 84 до 96 семян.
\[n=100\] \[p=0,9\] \[84\le k\le 96\] \[k_1=84\] \[k_2=96\] \[x''=\frac{k_2-np}{\sqrt{npq}}=\frac{96-100\cdot 0,9}{\sqrt{9}}=2\] \[x'=\frac{k_1-np}{\sqrt{npq}}=\frac{84-100\cdot 0,9}{\sqrt{9}}=-2\] \[P_{100}\left(84,96\right)=\left(x''\right)-\left(x'\right)=\left(2\right)-\left(-2\right)=2\left(2\right)=0,95\]Имеются таблицы, в которых помещены значения функции $\left(x\right)=\frac{1}{\sqrt{2}}e^{-\frac{x^2}{2}},$ соответствующие положительным значениям аргумента x. Для отрицательных значений аргумента пользуются теми же таблицами, так как функция $\varphi $(x) является чётной.
В театре, который вмещает 1000 зрителей, есть два входа, каждый из которых имеет свой гардероб. Какое должно быть минимальное количество мест в каждом гардеробе, что б с вероятностью $P\ge 0,99$ все зрители смогли раздеться в гардеробе того входа, через который они заходили? Примем во внимание, что зрители приходят парами и каждая пара независимо друг от друга выбирает один из входов с равным количеством вероятностей.
Пускай в каждом из двух гардеробов должно быть $2n$ мест. Через $2m$ обозначим число тех зрителей, которые воспользовались первым входом в театр, тогда вторым входом воспользовалось $1000-2m$ зрителей. В задаче необходимо что б выполнялось условие:
$P\left\{2m\le 2n,\ \ \ 1000-2m\le 2n\right\}\ge 0,99$ или
\[P\left\{1000-2n\le 2m\le 2n\right\}\ge 0,99; \] \[P\left\{500-n\le m\le n\right\}\ge 0,99\]Принимая во внимания, что $n=500,$ а $p=\frac{1}{2},$ за формулой $P_n\left(k_1;;k_2\right)=\left(x^{''}\right)-\left(x'\right),\ $получим
\[P\left\{500-n\le m\le n\right\}=\left(\frac{n-500\cdot \frac{1}{2}}{\sqrt{500\cdot \frac{1}{2}\cdot \frac{1}{2}}}\right)-\left(\frac{500-n-500\cdot \frac{1}{2}}{\sqrt{500\cdot \frac{1}{2}\cdot \frac{1}{2}}}\right)=\] \[=\left(\frac{n-250}{5\sqrt{5}}\right)-\left(-\frac{n+250}{5\sqrt{5}}\right)=\left(\frac{n-250}{5\sqrt{5}}\right)+\left(\frac{n-250}{5\sqrt{5}}\right)=\] \[=2\left(\frac{n-250}{5\sqrt{5}}\right)\ge 0,99.\]Искомое минимальное значение найдем с условия $\left(\frac{n-250}{5\sqrt{5}}\right)\ge 0,495.$
За таблицей которая имеется почти во всех книгах теории вероятности найдем, что $\frac{n-250}{5\sqrt{5}}=2,68.$ Откуда $n\ge 279.$
Значит, в каждом из гардеробов должно быть не меньше $279\cdot 2=558$ мест.
Вероятность того, что деталь не прошла контроль качества $p=0,2.$ Найти вероятность того, что среди 400 случайно выбранных деталей окажется непроверенными 70 деталей.
По условию задачи $p=0,2;\ \ q=1-0,2=0,8;\ \ \ n=400;\ \ k=70.$
Найдем
\[x_{70}=\frac{70-np}{\sqrt{npq}}=\frac{70-400\cdot 0,2}{\sqrt{400\cdot 0,2\cdot 0,8}}=-1,25.\]За локальной теоремой Лапласа, получим
\[P_{400}\left(70\right)=\frac{1}{\sqrt{400\cdot 0,2\cdot 0,8}}\cdot \left(-1,25\right).\]Значение $\left(-1,25\right)=\left(1,25\right)$ в таблице находим $\left(1,25\right)=0,8126.$ Тогда подставив это значение в предыдущую формулу получим $P_{400}\left(70\right)=\frac{0,1826}{8}\approx 0,023.$
