Понятие правильного многогранника
Введем вначале понятие многогранника и выпуклого многогранника.
Многогранником называется геометрическое тело в пространстве, которое ограниченно несколькими многоугольниками.
Если многогранник всегда будет лежать по одну сторону от любой плоскости его граней, то многогранник называется выпуклым (рис. 1).
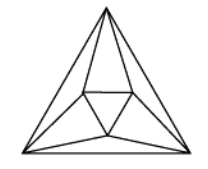
Рисунок 1. Выпуклый многогранник
Введем теперь непосредственно определение правильного многогранника.
Многогранник называется правильным, если он удовлетворяет следующим условиям:
-
Многогранник является выпуклым;
-
Все грани многогранника правильные, равные между собой многоугольники;
-
В каждой вершине многогранника сходится одинаковое число ребер.
Рассмотрим далее примеры классических правильных многогранников в курсе стереометрии.
Куб
Прямоугольный параллелепипед, все грани которого являются равными квадратами (рис. 2).
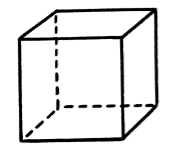
Рисунок 2. Куб
Квадраты, из которых составлен куб, называются гранями куба, стороны квадратов -- сторонами куба, а вершины квадратов -- вершинами куба.
где $a$ - сторона куба.
Правильный тетраэдр
Тетраэдр, гранями которого являются четыре правильных треугольника, называется правильным тетраэдром (рис. 3).
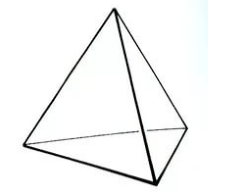
Рисунок 3. Правильный тетраэдр
Апофемой правильного тетраэдра называется высота её боковой грани.
Очевидно, что все апофемы равны между собой. Обозначим их через $l$.
где $a$ - сторона тетраэдра, $h$ - высота.
Правильный октаэдр
Выпуклый многогранник, состоящий из восьми правильных треугольников, называется октаэдром (рис. 4).
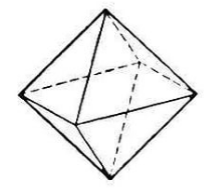
Рисунок 4.
где $a$ - сторона октаэдра.
Правильный додекаэдр
Выпуклый многогранник, состоящий из двадцати правильных треугольников, называется додекаэдром (рис. 5).
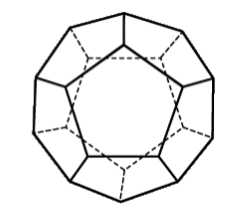
Рисунок 5.
где $a$ - сторона додекаэдра.
Правильный икосаэдр
Выпуклый многогранник, состоящий из двадцати правильных треугольников, называется икосаэдром (рис. 6).
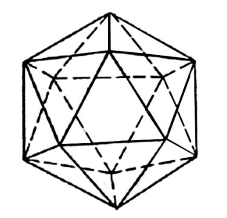
Рисунок 6.
где $a$ - сторона икосаэдра.
Пример задачи
Здесь мы предложим вам практическое задание.
На рисунке 7 приведены развертки различных правильных многогранников. Перерисуйте их на картонной бумаге (дополняя краешками для склеивания), вырежьте и склейте из них фигуры.
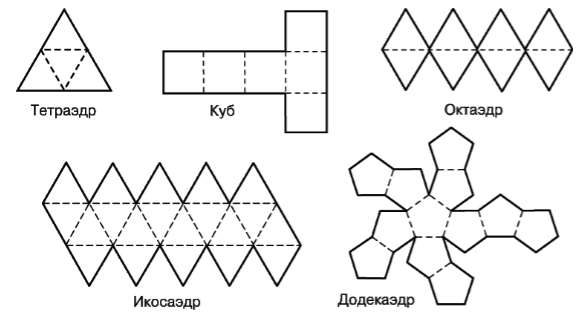
Рисунок 7.












