Угол между прямой и плоскостью

Источник статьи

Автор24 — учеба по твоим правилам

Понятие проекции фигуры на плоскость

Для введения понятия угла между прямой и плоскостью вначале необходимо разобраться в таком понятии, как проекция произвольной фигуры на плоскость.

Определение 1

Пусть нам дана произвольная точка $A$ . Точка $A_1$ называется проекцией точки $A$ на плоскость $\alpha$ , если она является основанием перпендикуляра, проведенного из точки $A$ на плоскость $\alpha$ (рис. 1).

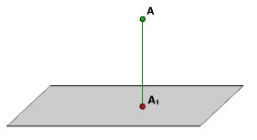
Рисунок 1. Проекция точки на плоскость

Определение 2

Пусть нам дана произвольная фигура $F$ . Фигура $F_1$ называется проекцией фигуры $F$ на плоскость $\alpha$ , составленная из проекций всех точек фигуры $F$ на плоскость $\alpha$ (рис. 2).

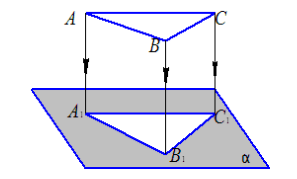
Рисунок 2. Проекция фигуры на плоскость

Теорема 1

Проекция не перпендикулярной плоскости прямой является прямая.

Доказательство.

Пусть нам дана плоскость $\alpha$ и пересекающая ее прямая $d$ , не перпендикулярная ей. Выберем на прямой $d$ точку $M$ и проведем её проекцию $H$ на плоскость $\alpha$ . Через прямую $(MH)$ проведем плоскость $\beta$ . Очевидно, что эта плоскость будет перпендикулярна плоскости $\alpha$ . Пусть они пересекаются по прямой $m$ . Рассмотрим произвольную точку $M_1$ прямой $d$ и проведем через нее прямую $(M_1H_1$ ) параллельно прямой $(MH)$ (рис. 3).

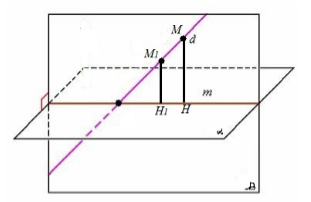
Рисунок 3.

Так как плоскость $\beta$ перпендикулярна плоскости $\alpha$ , то $M_1H_1$ перпендикулярно прямой $m$ , то есть точка $H_1$ - проекция точки $M_1$ на плоскость $\alpha$ . В силу произвольности выбора точки $M_1$ все точки прямой $d$ проецируются на прямую $m$ .

Рассуждая аналогично. В обратном порядке, будем получать, что каждая точка прямой $m$ является проекцией какой-либо точки прямой $d$ .

Значит, прямая $d$ проецируется на прямую $m$ .

Теорема доказана.

«Угол между прямой и плоскостью» 👇

Помощь эксперта по теме работы

Найти эксперта

Решение задач от ИИ за 2 минуты

Решить задачу

Помощь с рефератом от нейросети

Написать ИИ

Понятие угла между прямой и плоскостью

Определение 3

Угол между прямой, пересекающей плоскость и её проекцией на эту плоскость, называется углом между прямой и плоскостью (рис. 4).

Рисунок 4. Угол между прямой и плоскостью

Отметим здесь несколько замечаний.

Замечание 1

Если прямая перпендикулярна к плоскости. То угол между прямой и плоскостью равен $90^\circ$ .

Замечание 2

Если прямая параллельна или лежит в плоскости. То угол между прямой и плоскостью равен $0^\circ$ .

Примеры задач

Пример 1

Пусть нам дан параллелограмм $ABCD$ и точка $M$ , не лежащая в плоскости параллелограмма. Доказать, что треугольники $AMB$ и $MBC$ являются прямоугольными, если точка $B$ -- проекция точки $M$ на плоскость параллелограмма.

Доказательство.

Изобразим условие задачи на рисунке (рис. 5).

Рисунок 5.

Так как точка $B$ -- проекция точки $M$ на плоскость $(ABC)$ , то прямая $(MB)$ перпендикулярна плоскости $(ABC)$ . По замечанию 1, получаем, что угол между прямой $(MB)$ и плоскостью $(ABC)$ равен $90^\circ$ . Следовательно

$\angle MBC=MBA={90}^0$

Значит, треугольники $AMB$ и $MBC$ являются прямоугольными.

ч. т. д.

Пример 2

Дана плоскость $\alpha$ . Под углом $\varphi$ к этой плоскости проведен отрезок, начало которого лежит в данной плоскости. Проекция этого отрезка в два раза меньше самого отрезка. Найти величину $\varphi$ .

Решение.

Рассмотрим рисунок 6.

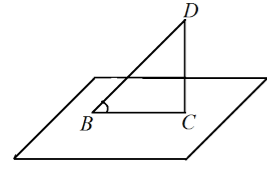
Рисунок 6.