Приближенное вычисление интегралов

Предпосылки приближенного интегрирования

Применение формулы Ньютона-Лейбница $\int \limits _{a}^{b}f\left(x\right)\cdot dx =F\left(b\right)-F\left(a\right)$ для вычисления определенного интеграла (ОИ) от непрерывной функции $f\left(x\right)$ возможно при условии, что для неё известна любая её первобразная $F\left(x\right)$. Но не для всех элементарных функций их первобразные также являются элементарными функциями. Например, это касается интеграла Пуассона $\int e^{-x^{2} } \cdot dx$, интегралов Френеля $\int \cos x^{2} \cdot dx$ и $\int \sin x^{2} \cdot dx$, интегрального логарифма $\int \frac{dx}{\ln x}$ и многих других. Кроме того, функция $f\left(x\right)$ может быть задана графиком или таблично. Во всех этих случаях воспользоваться формулой Ньютона-Лейбница невозможно.

Именно поэтому возникает потребность в использовании методов приближенного вычисления ОИ. В основе этих методов лежит геометрический смысл ОИ, а именно то, что он выражает площадь определенной криволинейной трапеции (КрТ). То есть, если удалось каким-то образом найти приближенное значение площади КрТ, то это число и принимается за приближенное значение соответствующего ОИ./

При приближенном вычислении ОИ некоторые проблемы возникают с обеспечением нужной точности интегрирования $\varepsilon$. Как будет видно из последующего изложения, приближенное интегрирование связано с разбиением отрезка интегрирования $\left[a,\; b\right]$ на определенное число $n$ равных частей. Чем больше $n$, тем точнее результат интегрирования. Поэтому приближенное интегрирование выполняют дважды: первый раз -- при разбиении на $n$ равных частей, второй раз -- при разбиении на $2\cdot n$ равных частей. Если оба результата интегрирования отличаются между собой более, чем на $\varepsilon$, то нужная точность считается не достигнутой. Нужно увеличить $n$ и повторить вычисления.

Формулы приближенного интегрирования

В приближенном интегрировании наиболее популярны формулы прямоугольников, трапеций и Симпсона (парабол).

Разбиваем отрезок интегрирования $\left[a,\; b\right]$ на $n$ равных частей. Ширина каждой части $h=\frac{b-a}{n}$. Точки разбиения $y_{i} =f\left(x_{i} \right),\, \; i=0,1,\ldots ,n$. При этом $x_{0} =a$, $x_{n} =b$.

1. Формула левых прямоугольников имеет вид:
$$I_{} =\int \limits _{a}^{b}f\left(x\right)\cdot dx \approx h\cdot \sum \limits _{i=0}^{n-1}f\left(x_{i} \right) =h\cdot \left(y_{0} +y_{1} +y_{2} +\ldots +y_{n-2} +y_{n-1} \right).$$

Работу формулы демонстрирует нижеследующий рисунок. Площадь левого прямоугольника $aAB_{1} b$ принимается в качестве приближенного значения площади КрТ $aABb$.



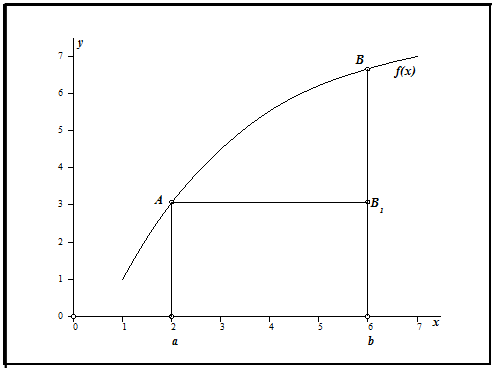
Формула правых прямоугольников имеет вид:

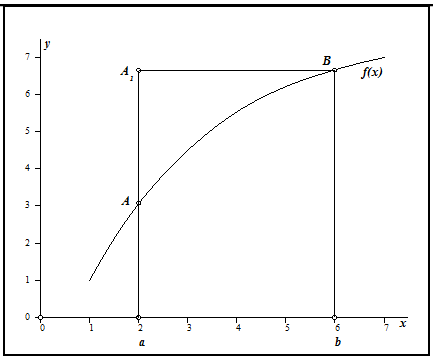
$$I_{} =\int \limits _{a}^{b}f\left(x\right)\cdot dx \approx h\cdot \sum \limits _{i=1}^{n}f\left(x_{i} \right) =h\cdot \left(y_{1} +y_{2} +y_{3} +\ldots +y_{n-1} +y_{n} \right).$$

Площадь правого прямоугольника $aA_{1} Bb$ принимается в качестве приближенного значения площади КрТ $aABb$.



2. Формула трапеций имеет вид:
$$I_{"} =\int \limits _{a}^{b}f\left(x\right)\cdot dx \approx \frac{h}{2} \cdot \sum \limits _{i=1}^{n}\left(f\left(x_{i-1} \right)+f\left(x_{i} \right)\right) =$$ $$=\frac{h}{2} \cdot \left(y_{0} +2\cdot y_{1} +2\cdot y_{2} +\ldots +2\cdot y_{n-1} +y_{n} \right).$$

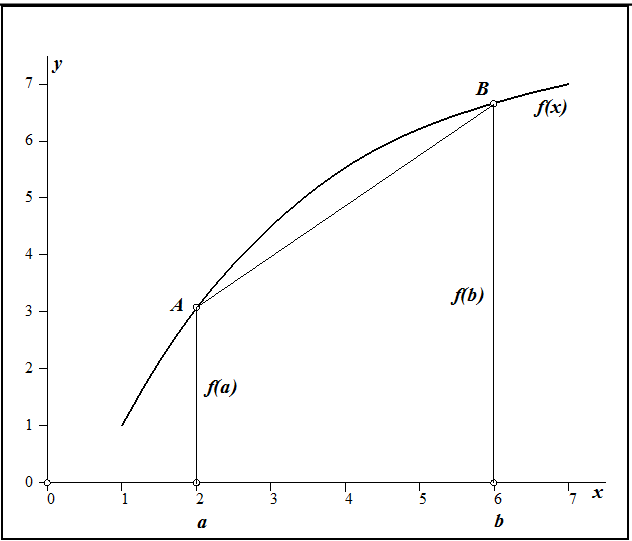
Площадь обычной прямолинейной трапеции $aABb$ принимается в качестве приближенного значения площади КрТ $aABb$.



3. Отрезок интегрирования $\left[a,\; b\right]$ следует разбить на четное число $n$ равных частей.

Формула Симпсона имеет вид:

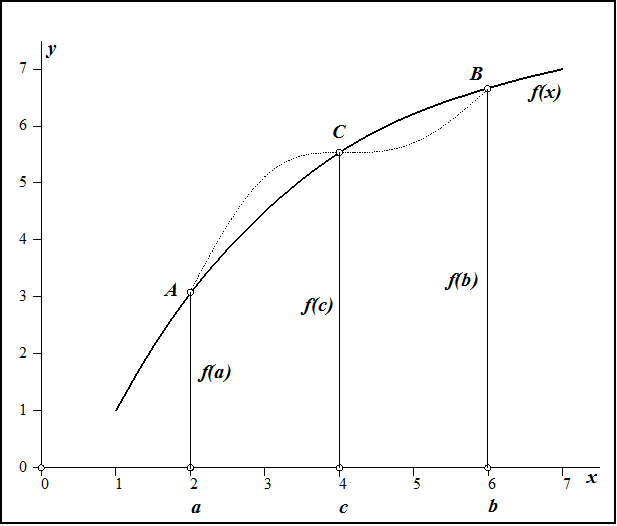
$$I_{!} =\int \limits _{a}^{b}f\left(x\right)\cdot dx \approx$$ $$\approx \frac{h}{3} \cdot \left(y_{0} +y_{n} +2\cdot \left(y_{2} +y_{4} +\ldots +y_{n-2} \right)+4\cdot \left(y_{1} +y_{3} +\ldots +y_{n-1} \right)\right).$$

Площадь КрТ $aACBbc$ принимается в качестве приближенного значения площади КрТ $aABb$.