Понятие касательной к окружности
Окружность имеет три возможных взаимных расположений относительно прямой:
-
Если расстояние от центра окружности до прямой меньше радиуса, то прямая имеет две точки пересечения с окружностью.
-
Если расстояние от центра окружности до прямой равно радиусу, то прямая имеет две точки пересечения с окружностью.
-
Если расстояние от центра окружности до прямой больше радиуса, то прямая имеет две точки пересечения с окружностью.
Введем теперь понятие касательной прямой к окружности.
Касательной к окружности называется прямая, которая имеет с ней одну точку пересечения.
Общая точка окружности и касательной называется точкой касания (рис 1).
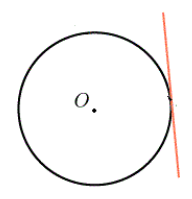
Рисунок 1. Касательная к окружности
Теоремы, связанные с понятием касательной к окружности
Теорема о свойстве касательной: касательная к окружности перпендикулярна к радиусу, проведенному в точку касания.
Доказательство.
Рассмотрим окружность с центром $O$. Проведем в точке $A$ касательную $a$. $OA=r$ (Рис. 2).
Докажем, что $a\bot r$
Будем доказывать теорему методом «от противного». Предположим, что касательная $a$ не перпендикулярна радиусу окружности.
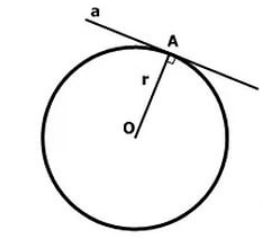
Рисунок 2. Иллюстрация теоремы 1
То есть $OA$ - наклонная к касательной. Так как перпендикуляр к прямой $a$ всегда меньше наклонной к этой же прямой, то расстояние от центра окружности до прямой меньше радиуса. Как нам известно, в этом случае прямая имеет две точки пересечения с окружностью. Что противоречит определению касательной.
Следовательно, касательная перпендикулярна к радиусу окружности.
Теорема доказана.
Обратная теореме о свойстве касательной: Если прямая, проходящая через конец радиуса какой-либо окружности перпендикулярна радиусу, то данная прямая является касательной к этой окружности.
Доказательство.
По условию задачи мы имеем, что радиус -- перпендикуляр, проведенный из центра окружности к данной прямой. Следовательно, расстояние от центра окружности до прямой равняется длине радиуса. Как мы знаем, в этом случае окружность имеет только одну точку пересечения с этой прямой. По определению 1 и получаем, что данная прямая -- касательная к окружности.
Теорема доказана.
Отрезки касательных к окружности, проведенные из одной точки, равны и составляют равные углы с прямой, проходящей через эту точку и центр окружности.
Доказательство.
Пусть дана окружность с центром в точке $O$. Из точки $A$ (лежащей все окружности) проведены две различные касательные. Из точки касания соответственно $B$ и $C$ (Рис. 3).
Докажем, что $\angle BAO=\angle CAO$ и что $AB=AC$.
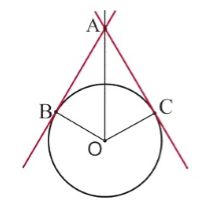
Рисунок 3. Иллюстрация теоремы 3
По теореме 1, имеем:
Следовательно, треугольники $ABO$ и $ACO$ -- прямоугольные. Так как$OB=OC=r$, а гипотенуза $OA$ -- общая, то эти треугольники равны по гипотенузе и катету.
Отсюда и получаем, что $\angle BAO=\angle CAO$ и $AB=AC$.
Теорема доказана.
Пример задачи на понятие касательной к окружности
Дана окружность с центром в точке $O$ и радиусом $r=3\ см$. Касательная $AC$ имеет точку касания $C$. $AO=4\ см$. Найти $AC$.
Решение.
Изобразим вначале все на рисунке (Рис. 4).
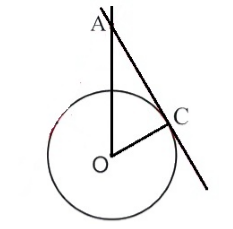
Рисунок 4.
Так как $AC$ касательная, а $OC$ радиус, то по теореме 1, получаем, что$\angle ACO={90}^{{}^\circ }$. Получили, что треугольник $ACO$ -- прямоугольный, значит, по теореме Пифагора, имеем:
\[{AC}^2={AO}^2+r^2\] \[{AC}^2=16+9\] \[{AC}^2=25\] \[AC=5\]Ответ: $5$.












