Понятие вписанного и центрально угла
Введем сначала понятие центрального угла.
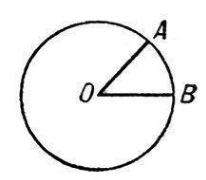
Угол, вершина которого лежит в центре окружности называется центральным углом (рис. 1).
 Центральный угол">
Центральный угол">
Рисунок 1. Центральный угол
Отметим, что градусная мера центрального угла равна градусной мере дуги, на которую он опирается.
Введем теперь понятие вписанного угла.
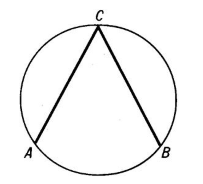
Угол, вершина которого лежит на окружности и стороны которого пересекают эту же окружность, называется вписанным углом (рис. 2).
 Вписанный угол">
Вписанный угол">
Рисунок 2. Вписанный угол
Теорема о вписанном угле
Градусная мера вписанного угла равняется половине градусной меры дуги, на которую он опирается.
Доказательство.
Пусть нам дана окружность с центром в точке $O$. Обозначим вписанный угол $ACB$ (рис. 2). Возможны три следующих случая:
- Луч $CO$ совпадает с какой либо стороной угла. Пусть это будет сторона $CB$ (рис. 3).
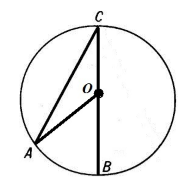
Рисунок 3.
В этом случае дуга $AB$ меньше ${180}^{{}^\circ }$, следовательно, центральный угол $AOB$ равен дуге $AB$. Так как $AO=OC=r$, то треугольник $AOC$ равнобедренный. Значит, углы при основании $CAO$ и $ACO$ равны между собой. По теореме о внешнем угле треугольника, имеем:
- Луч $CO$ делит внутренний угол на два угла. Пусть он пересекает окружность в точке $D$ (рис. 4).
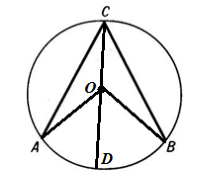
Рисунок 4.
Рассмотрим отдельно углы $ACD$ и $DCB$. По доказанному в пункте 1, получим
Получаем
- Луч $CO$ не делит внутренний угол на два угла и не совпадает ни с одной его стороной (Рис. 5).
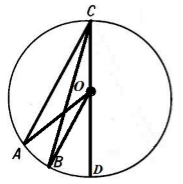
Рисунок 5.
Рассмотрим отдельно углы $ACD$ и $DCB$. По доказанному в пункте 1, получим
Получаем
Теорема доказана.
Приведем следствия из данной теоремы.
Следствие 1: Вписанные углы, которые опираются на одну и туже дугу равны между собой.
Следствие 2: Вписанный угол, который опирается на диаметр -- прямой.
Пример задачи на использование понятий центрально и вписанного углов
Найти градусные меры вписанных углов, изображенных на рисунке (рис.6).
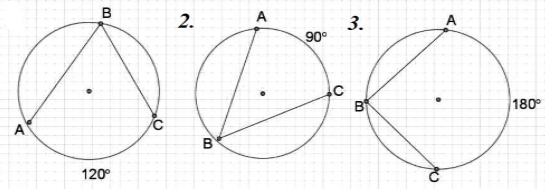
Рисунок 6.
Решение.
-
По теореме 1, имеем:
\[\angle ABC=\frac{{120}^0}{2}={60}^0\] -
По теореме 1, имеем:
\[\angle ABC=\frac{{90}^0}{2}={45}^0\] -
Из следствия 2 сразу получаем, что искомый угол -- прямой.












