Напомним для начала следующие факты:
Вспомним формулу для нахождения вероятности того, что отклонение, распределенной по нормальному закону непрерывной случайной величины $X$, от математического ожидания $a$ по абсолютной величине (то есть по модулю) будет меньше $\delta $:
среднееНапомним таблицу нахождения значений интегральной функции (таблица 1)
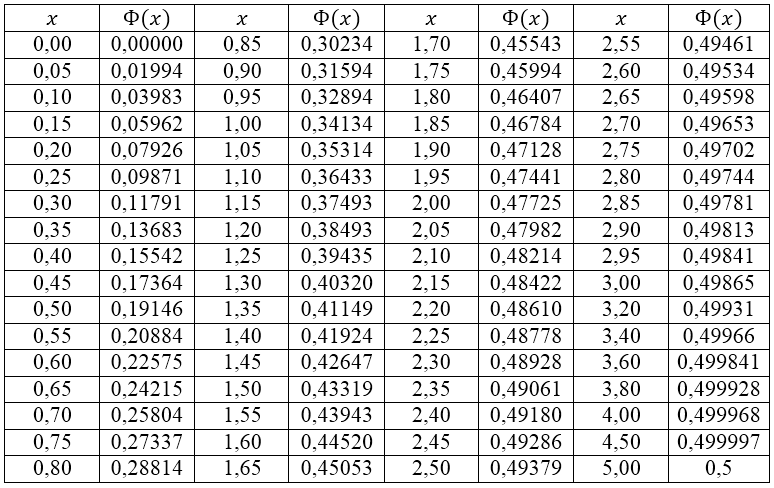
Рисунок 1. Значения интегральной функции $Ф(x)$.
Теперь найдем, чему будет равна вероятность того, что отклонение, распределенной по нормальному закону непрерывной случайной величины $X$, от математического ожидания $a$ по абсолютной величине (то есть по модулю) будет меньше $3\sigma $, то есть:
Геометрически этот факт можно представить следующим образом:
Рисунок 2.
Из всего вышесказанного сформулируем следующее правило:
Правило трёх сигм: Если непрерывная случайная величина $X$ распределена по нормальному закону, то абсолютная величина её отклонения от математического ожидания $a$ не превосходит утроенного значения среднего квадратического отклонения $\sigma $.
Примеры решения задач на применение правила трех сигм
Длина изготавливаемого стержня подчинена нормальному закону распределения. Математическое ожидание $a=1$ м, а среднее математическое отклонение $\sigma =0,01$ м. Найти границы, пределах которых гарантируется длина стержня.
Решение.
Для решения задачи воспользуемся правилом трех сигм:
\[P\left(|X-a|Текущая цена на молоко подчинена нормальному закону распределения. Математическое ожидание $a=25$ рублей, а среднее математическое отклонение $\sigma =1$ рубль. Найти границы, в которых будет находиться текущая цена нам молоко.
Решение.
Для решения задачи воспользуемся правилом трех сигм:
\[P\left(|X-a|Так как случайная величина (цена) распределена по нормальному закону, то \[P\left(\left|X-25\right|Ответ: (22,28).На заводе изготавливают шурупы для ноутбуков. Размер диаметра шурупа распределен по нормальному закону распределения с математическим ожиданием $a=0,2\ $см и средним квадратическим отклонением $\sigma =0,02$ мм. В каких границах можно практически 100\% гарантировать размер шурупа?
Решение.
Вначале приведем все величины к одному измерению:
$a=0,2\ $см$=2$ мм.
Так как случайная величина подчинена нормальному закону распределения, то мы можем применить правило трех сигм:
\[P\left(\left|X-2\right|Ответ: (1,94, 2,06)










