Прямая
Понятие прямой, также как и понятие точки является основными понятиями геометрии. Как известно основные понятия не определяется. Это не является и исключением для понятия прямой. Поэтому рассмотрим суть этого понятия через его построение.
Возьмем линейку и, не отрывая карандаша, проведем линию произвольной длины (рис. 1).
Полученную линию мы и будем называть прямой. Однако тут необходимо отметить, что это не вся прямая, а только её часть. Всю же прямую построить не имеется возможным, она является бесконечной на обоих своих концах.
Прямые будем обозначать маленькой латинской буквой, либо двумя её точками в круглых скобках (рис. 2).
Понятия прямой и точки связаны тремя аксиомами геометрии:
Аксиома 1: Для каждой произвольной прямой существует как минимум две точки, которые на ней лежат.
Аксиома 2: Можно найти как минимум три точки, которые не будут лежать на одной и той же прямой.
Аксиома 3: Через $2$ произвольные точки всегда проходит прямая, причем эта прямая единственна.
Для двух прямых актуально их взаимное расположение. Возможны три случая:
- Две прямые совпадают. В этом случае каждая точка одной будет также и точкой другой прямой.
- Две прямые пересекаются. В этом случае только какая-то одна точка из одной прямой будет также принадлежать и другой прямой.
- Две прямые параллельны. В этом случае у каждой из этих прямых свой набор различных друг от друга точек.
В этой статье мы не будем подробно останавливаться на этих понятиях.
Отрезок
Пусть нам дана произвольная прямая и две точки, принадлежащие ей. Тогда
Отрезком будет называться часть прямой, которая ограничена двумя ее произвольными различными точками.
Точки, которыми ограничен отрезок в рамках определения 1 называются концами этого отрезка.
Отрезки будем обозначать двумя её точками концов в квадратных скобках (рис. 3).
Сравнение отрезков
Рассмотрим два произвольных отрезка. Очевидно, что они могут быть либо равными, либо неравными. Чтобы разобраться в этом, нам нужна следующая аксиома геометрии.
Аксиома 4: Если оба конца двух различных отрезков совпадут при их наложении, то такие отрезки будут равными.
Итак, для сравнения выбранных нами отрезков (обозначим их отрезок 1 и отрезок 2) наложим конец отрезка 1 на конец отрезка 2, так, чтобы, отрезки оставались по одну сторону от этих концов. После такого наложения возможны два следующих случая:
Вторые концы этих отрезков также совпадут. В таком случае по аксиоме 5 мы получим, что такие отрезки будут равны друг другу (рис. 4).
Вторые корцы не совпадут. Здесь, без ограничения общности, будем считать, что конец отрезка 1 будет принадлежать отрезку 2. Тогда здесь мы говорим, что данные отрезки не равны, причем отрезок 1 короче отрезка 2.
Длина отрезка
Помимо сравнения одних отрезков с другими также часто необходимо измерение отрезков. Измерить отрезок означает найти его длину. Для этого необходимо выбрать какой-то «эталонный» отрезок, который мы будем принимать за единицу ( к примеру отрезок, длина которого равняется 1 сантиметру). После выбора такого отрезка мы проводим с ним сравнение отрезков, длину которого нужно найти. Рассмотрим пример.
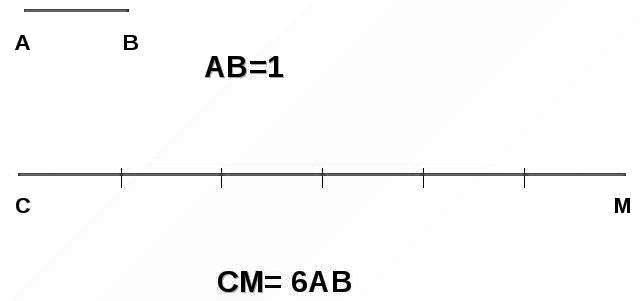
Найти длину следующего отрезка
если следующий отрезок равняется 1
Решение.
Для его измерения возьмем за эталон отрезок $[AB]$. Будем откладывать его на отрезок $[CM]$. Получим:
Ответ: $6$ см.
Понятие длины отрезка связаны со следующими аксиомами геометрии:
Аксиома 5: Выбрав определенную единицу измерения отрезков, длина любого отрезка будет положительна.
Аксиома 6: Выбрав определенную единицу измерения отрезков, мы можем для любого положительного числа найти отрезок, у которого длина равняется данному числу.
После определения длины отрезков у нас появляется второй способ для сравнения отрезков. Если при одном и том же выборе единицы длины отрезок $1$ и отрезок $2$ будут иметь одинаковую длину, то такие отрезки будут называться равными. Если же, без ограничения общности, отрезок 1 будет иметь длину по числовому значению меньше длины отрезка $2$, то отрезок $1$ будет меньше отрезка $2$.
Самым простым способом измерения длины отрезков является измерение, с помощью линейки.
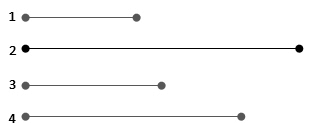
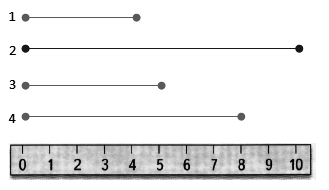
Записать длины следующих отрезков:
Решение.
Измерим их с помощью линейки:
Получим.
Ответ:
- $4$ см.
- $10$ см.
- $5$ см.
- $8$ см.










![Отрезок [AB]](/assets/files/handbook/images/56/e8/56e842f0a1f35ce72c937dc5f2c62356)