Частично использовать разложение на множители разность степеней мы уже умеем - при изучении темы «Разность квадратов» и «Разность кубов» мы научились представлять как произведение разность выражений, которые можно представить как квадраты или как кубы некоторых выражений или чисел.
Формулы сокращенного умножения
По формулам сокращенного умножения:
разность квадратов можно представить как произведение разности двух чисел или выражений на их сумму
Разность кубов можно представить как произведение разности двух чисел на неполный квадрат суммы
Переход к разности выражений в 4 степени
Опираясь на формулу разности квадратов, попробуем разложить на множители выражение $a^4-b^4$
Вспомним, как возводится степень в степень - для этого основание остается прежним, а показатели перемножаются, т. е ${(a^n)}^m=a^{n*m}$
Тогда можно представить:
$a^4={{(a}^2)}^2$
$b^4={{(b}^2)}^2$
Значит, наше выражение можно представить, как $a^4-b^4={{(a}^2)}^2$-${{(b}^2)}^2$
Далее можно заметить, что теперь многочлен представляет собой разность квадратов одночленов $a^2$ и $b^2$ .Разложим многочлен на множители как произведение разности одночленов на их сумму
Теперь в первой скобке мы вновь получили разность чисел, значит вновь можно разложить на множители как произведение разности двух чисел или выражений на их сумму: $a^2-b^2=\left(a-b\right)(a+b)$.
Исходное выражение принимает вид
Теперь вычислим произведение второй и третьей скобок используя правило произведения многочленов, - умножим каждый член первого многочлена на каждый член второго многочлена и сложим результат. Для этого сначала первый член первого многочлена - $a$ - умножим на первый и второй член второго (на $a^2$ и $b^2$),т.е. получим $a\cdot a^2+a\cdot b^2$, затем второй член первого многочлена -$b$- умножим на первый и второй члены второго многочлена (на $a^2$ и $b^2$),т.е. получим $b\cdot a^2 + b\cdot b^2$ и составим сумму получившихся выражений
$\left(a+b\right)\left(a^2+b^2\right)=a\cdot a^2+a\cdot b^2+ b \cdot a^2 + b\cdot b^2 = a^3+ab^2+a^2b+b^3$
Запишем разность одночленов 4 степени с учетом вычисленного произведения:
$a^4-b^4={{(a}^2)}^2$-${{(b}^2)}^2={(a}^2-b^2)(a^2+b^2)$=$\ \left(a-b\right)(a+b)(a^2+b^2)\ $=
Переход к разности выражений в 6 степени
Опираясь на формулу разности квадратов попробуем разложить на множители выражение $a^6-b^6$
Вспомним, как возводится степень в степень - для этого основание остается прежним, а показатели перемножаются, т. е ${(a^n)}^m=a^{n\cdot m}$
Тогда можно представить:
$a^6={{(a}^3)}^2$
$b^6={{(b}^3)}^2$
Значит, наше выражение можно представить, как $a^6-b^6={{(a}^3)}^2-{{(b}^3)}^2$
Далее можно заметить, что теперь многочлен представляет собой разность квадратов одночленов $a^2$ и $b^2$ .Разложим многочлен на множители как произведение разности одночленов на их сумму
В первой скобке мы получили разность кубов одночленов, во второй сумму кубов одночленов, теперь вновь можно разложить на множители разность кубов одночленов как произведение разности двух чисел на неполный квадрат суммы $a^3-b^3=\left(a-b\right)(a^2+ab+b^2)$
Исходное выражение принимает вид
$a^6-b^6={(a}^3-b^3)\left(a^3+b^3\right)=\left(a-b\right)(a^2+ab+b^2)(a^3+b^3)$
Вычислим произведение второй и третье скобок используя правило произведения многочленов, - умножим каждый член первого многочлена на каждый член второго многочлена и сложим результат.
$(a^2+ab+b^2)(a^3+b^3)=a^5+a^4b+a^3b^2+a^2b^3+ab^4+b^5$
Запишем разность одночленов 6 степени с учетом вычисленного произведения:
$a^6-b^6={(a}^3-b^3)\left(a^3+b^3\right)=\left(a-b\right)(a^2+ab+b^2)(a^3+b^3)=(a-b)(a^5+a^4b+a^3b^2+a^2b^3+ab^4+b^5)$
Разложение на множители разности степеней
Проанализируем формулы разности кубов, разности $4$ степеней, разности $6$ степеней
Мы видим, что в каждом из данных разложений присутствует некоторая аналогия, обобщая которую получим:
Разложить на множители ${32x}^{10}-{243y}^{15}$
Решение: Сначала представим каждый одночлен как некоторый одночлен в 5 степени:
\[{32x}^{10}={(2x^2)}^5\]\[{243y}^{15}={(3y^3)}^5\]Используем формулу разности степеней
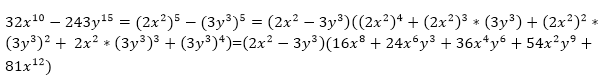
Рисунок 1.












