Сущность координатного метода для решения геометрических задач
Координатный метод решения задач основан на решении задач с помощью введения в задачу системы координат. В этой статье мы не будем делать акцент на том, как именно вводятся координаты, предполагая, что с этим понятием мы уже знакомы.
Метод координат для решения геометрических задач основан на следующих основных утверждениях.
Утверждение 1: Координаты вектора равны разности соответствующих координат конца вектора и его начала.
Утверждение 2: Координата середины отрезка равна полусумме соответствующих координат его концов.
Утверждение 3: Длина вектора с координатами $\left\{x,\ y\right\}$ равняется
Утверждение 4: Расстояние между двумя точками с координатами $\left\{x_1,\ y_1\right\}$ и $\{x_2,\ y_2\}$ равняется
Общая схема для решения геометрических задач координатным методом
При решении геометрических задач координатным методом рекомендуется пользоваться следующей схемой:
-
Провести анализ условия задачи:
а) Выяснить в какой системе координат (двумерной или трехмерной) рассматривается данная задача;
б) Записать, что нам дано, что нужно найти или доказать, а также построить чертеж по условию задачи.
-
Перевести условие задачи к координатам в выбранной системе координат.
-
Составить соотношения, соответствующие тому, что дано в задаче и привести их к соотношениям, соответствующим требованиям задачи.
-
Перевести полученный результат на геометрический язык.
Примеры типов задач, которые решаются векторным методом
Приведем теперь примеры простейших задач, решаемых с помощью координатного метода (Не приводя их решений).
-
Вычисление координат вектора по координатам его начала и конца.
-
Задачи о делении отрезка в данном отношении.
-
Задачи на доказательство принадлежности трех точек одной прямой.
-
Задачи на доказательство принадлежности четырех точек одной плоскости.
-
Вычисление расстояние между двумя точками.
-
Задачи на вычисление площадей и объемов геометрических фигур.
Некоторые из результатов этих задач приведены нами выше в качестве основных утверждений, используемых при решении геометрических задач координатным методом.
Примеры задач на применение векторного метода
Доказать, что середина гипотенузы прямоугольного треугольника равноудалена от всех вершин этого треугольника.
Решение.
Пусть нам дан треугольник $ABC$ с прямым углом $C$. $M$ - центр гипотенузы $AB$. Введем систему координат следующим образом (рис. 1).
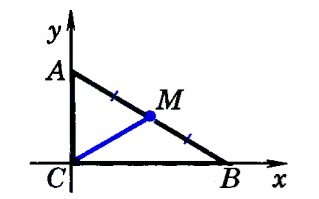
Рисунок 1.
Введем следующие координаты по данной системе координат:
\[C=\left\{0,0\right\},\ A=\left\{0,y\right\},\ B=\{x,0\}\]Используя утверждение 2, получим:
\[M=\left\{\frac{0+x}{2},\ \frac{y+0}{2}\right\}=\left\{\frac{x}{2},\ \frac{y}{2}\right\}\]Найдем расстояния от этой точки до каждой из вершин, используя утверждение 4:
\[AM=\sqrt{{\left(0-\frac{x}{2}\right)}^2+{\left(y-\frac{y}{2}\right)}^2}=\frac{\sqrt{x^2+y^2}}{2}\] \[BM=\sqrt{{\left(x-\frac{x}{2}\right)}^2+{\left(0-\frac{y}{2}\right)}^2}=\frac{\sqrt{x^2+y^2}}{2}\] \[CM=\sqrt{{\left(0-\frac{x}{2}\right)}^2+{\left(0-\frac{y}{2}\right)}^2}=\frac{\sqrt{x^2+y^2}}{2}\]Следовательно, $AM=BM=CM$.
ч. т. д.
Доказать, что сумма квадратов всех сторон произвольного параллелограмма равняется сумме квадратов его диагоналей.
Решение.
Пусть нам дан параллелограмм $ABCD$. Введем систему координат следующим образом (рис. 2).
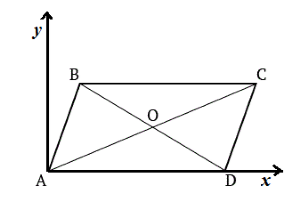
Рисунок 2.
Введем следующие координаты по данной системе координат:
\[A=\left\{0,0\right\},\ B=\left\{a,b\right\},\ D=\left\{c,0\right\},\ C=\{a+c,b\}\]Используя утверждение 4, получим:
\[{AB}^2={CD}^2={(a-0)}^2+{(b-0)}^2=a^2+b^2\] \[{AD}^2={BC}^2={(c-0)}^2+{(0-0)}^2=c^2\] \[{AB}^2+{CD}^2+{AD}^2+{BC}^2=2(a^2+b^2+c^2)\] \[{AC}^2={(a+c-0)}^2+{(b-0)}^2=a^2+2ac+c^2+b^2\] \[{BD}^2={(c-a)}^2+{(0-b)}^2=c^2-2ac+a^2+b^2\] \[{AC}^2+{BD}^2=a^2+2ac+c^2+b^2+c^2-2ac+a^2+b^2=2(a^2+b^2+c^2)\]Следовательно,
\[{AB}^2+{CD}^2+{AD}^2+{BC}^2={AC}^2+{BD}^2\]ч. т. д.












