Функция прямой пропорциональности
Для начала вспомним, что является функцией прямой пропорциональности.
Две не равные нулю величины называются прямо пропорциональными, если их отношение равно не равному нулю числу:
\[\frac{y}{x}=k\]Если теперь предположить, что они могут равнять нулю и умножить обе части на $x$ получим выражение вида $y=kx$. Это выражение будет называться функцией прямой пропорциональности.
Определение линейной функции
Будем рассматривать определение линейной функции с помощью её аналитического задания. Для ее определения используем аналитическое выражение функции прямой пропорциональности. Прибавив к правой части данного выражения какую-либо константу (включая ноль) и получим линейную функцию, то есть
Линейной функцией называется выражение $y=kx+b$, где $k$ не равно нулю.
Графиком линейной функции является прямая. Коэффициент $k$ является угловым коэффициентом данной прямой.
Рассмотрим следующий рисунок:
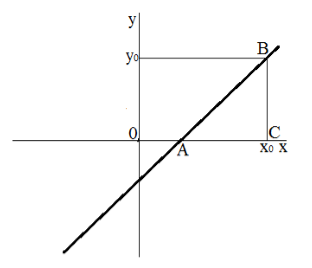
Рисунок 1.
Возьмем для рассмотрения $\triangle ABC$. В нем длина $BC=kx_0+b$. Далее разрешим по отношению к $x$ следующее уравнение
То есть ведичина $AC=x_0+\frac{b}{k}$. Найдем сдедующее отношение:
С другой стороны $\frac{BC}{AC}=tg\angle A$.
Следовательно,
Геометрический смысл коэффициента $k$. Угловой коэффициент прямой $k$ равняется тангенсу угла наклона данной прямой к оси $Ox$.
Исследование линейной функции $f(x)=kx+b$ и её график
Рассмотрим два случая:
-
$k >0$.
- $D\left(f\right)=R$.
- $E\left(f\right)=R$
- $f\left(-x\right)=-kx+b$, следовательно, данная функция -- функция общего вида.
- При $x=0,f\left(0\right)=b$. При $y=0,0=kx+b,\ x=-\frac{b}{k}$.
Следовательно, данная функция пересекает оси в точках: $\left(-\frac{b}{k},0\right)$ и $\left(0,\ b\right)$
- $f'\left(x\right)={\left(kx+b\right)}'=k>0$. Функция возрастает при $x=R$. Экстремумов нет.
- $f^{''}\left(x\right)=k'=0$. Функция не имеет перегибов и не является ни выпуклой, ни вогнутой.
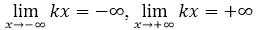
Рисунок 2.- График изображен на рисунке 2.
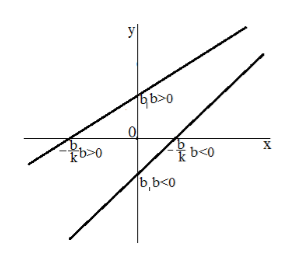
Рисунок 3. -
$k
- $D\left(f\right)=R$.
- $E\left(f\right)=R$.
- $f\left(-x\right)=-kx+b$, следовательно, данная функция -- функция общего вида.
- При $x=0,f\left(0\right)=b$. При $y=0,0=kx+b,\ x=-\frac{b}{k}$.
Следовательно, данная функция пересекает оси в точках: $\left(-\frac{b}{k},0\right)$ и $\left(0,\ b\right)$\textit{}
- $f'\left(x\right)={\left(kx\right)}'=k
- $f^{''}\left(x\right)=k'=0$. Функция не имеет перегибов и не является ни выпуклой, ни вогнутой.
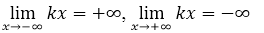
Рисунок 4.- График изображен на рисунке 3.
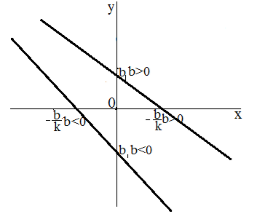
Рисунок 5.
Пример задачи
Построить график линейной функции $y=2x+3$
Приведем табличный способ задания функции

Рисунок 6.
Остается провести прямую через данные точки. Получим
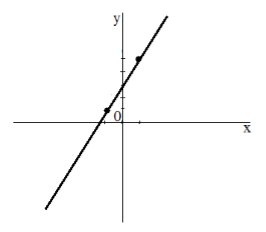
Рисунок 7.











