
Бином Ньютона
Одними из основных формул сокращенного умножения является формулы квадрата суммы и квадрата разности двух одночленов.
Данные формулы можно вывести с помощью Бинома Ньютона.
Формула бинома Ньютона для натуральных чисел имеет следующий вид:
Здесь $C^0_n,\ C^1_n,\dots ,C^{n-1}_n,C^n_n$ -- коэффициенты Бинома Ньютона.
Коэффициенты разложения Бинома Ньютона можно находить с помощью треугольника Паскаля.
Треугольник Паскаля имеет следующую структуру (рис. 1).
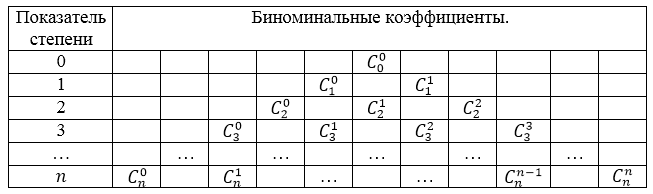
Рисунок 1. Структура треугольника Паскаля
Значения коэффициентов треугольника паскаля приведены в следующей таблице (рис. 2):
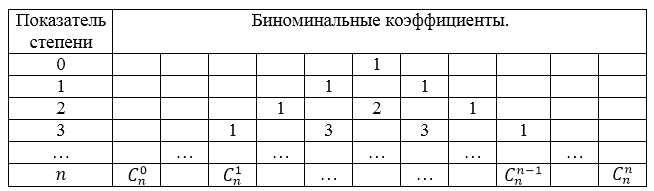
Рисунок 2. Коэффициенты треугольника Паскаля
Формула квадрата суммы
Выведем с использованием формулы Бинома Ньютона формулу квадрата суммы ${(a+b)}^2$. Из формулы Бинома Ньютона получаем:
Используя таблицу 2, получим:
Таким образом, квадрат суммы двух выражений равен сумме квадрата первого выражения с удвоенным произведением первого выражения на второе и квадратом второго выражения:
Пример 1: возвести в квадрат $(2x+3y)$
Используя формулу квадрата суммы, получим:
!!! Здесь стоит обратить особое внимание, что формулу надо применяя к одночленам, входящим в сумму, целиком. Типичной ошибкой в данном случае бывает то, что зачастую в квадрат возводят только часть одночлена (к примеру, возводят не $2x$ целиком, а только $x$, что является ошибкой!!!)
Формула квадрата разности
Найдем теперь формулу разности суммы. Для этого вначале представим выражение в следующем виде:
Воспользуемся формулой Бинома Ньютона:
Используя таблицу 2, получим:
Таким образом, квадрат разности двух выражений равен сумме квадрата первого выражения с квадратом второго выражения без удвоенного произведения первого выражения на второе:
Примеры задач на использование формул квадрата суммы и разности
Выполнить возведение в квадрат:
а) ${(-9a+4b)}^2$
б) ${(-8a-5b)}^2$
в) ${(x^2-7)}^2$
Решение:
а) ${(-9a+4b)}^2$
Поменяем одночлены, стоящие в скобке, местами:
\[{(-9a+4b)}^2={(4b-9a)}^2\]Воспользуемся формулой квадрата разности:
\[{(4b-9a)}^2={(4b)}^2-2\cdot 4b\cdot 9a+{(9a)}^2={16b}^2-72ab+{81a}^2\]б) ${(-8a-5b)}^2$
Так как квадрат всегда положительное число, то получим:
\[{(-8a-5b)}^2={(8a+5b)}^2\]Воспользуемся формулой квадрата суммы:
\[{(8a+5b)}^2={(8a)}^2+2\cdot 5b\cdot 8a+{(5b)}^2={64a}^2+80ab+{25b}^2\]в) ${(x^2-7)}^2$
Воспользуемся формулой квадрата разности:
\[{(x^2-7)}^2={(x^2)}^2-2\cdot x^2\cdot 7+7^2=x^4-14x^2+49\]Представить в виде квадрата:
а) $4a^2+12a+9$
б) $x^2-20xy^2+100y^4$
Решение:
а) $4a^2+12a+9$
Воспользуемся формулой квадрата суммы:
\[4a^2+12a+9={(2a)}^2+2\cdot 2a\cdot 3+3^2=(2a+3)^2\]б) $x^2-20xy^2+100y^4$
Воспользуемся формулой квадрата разности:
\[x^2-20xy^2+100y^4=x^2-2\cdot x\cdot 10y^2+{(10y)}^2=(x-10y)^2\]















