Основные определения
Понятие выборки используется, когда надо изучить какие-либо свойства совокупности объектов. Свойства объектов можно разделить на качественные и количественные.
Пусть нам необходимо изучить совокупность партии сметаны. Тогда качественным признаком может служить срок её годности, а количественным процент содержания жиров в данной сметане.
Совокупность или выборка может быть разделена на генеральную и выборочную.
Генеральная совокупность -- совокупность случайно отобранных объектов данного вида, над которыми проводят наблюдения с целью получения конкретных значений случайной величины, проводимых в неизменных условиях при изучении одной случайной величины данного вида.
Выборочная совокупность -- часть отобранных объектов из генеральной совокупности.
С понятием совокупности также связано понятие объема данной совокупности.
Объем совокупности -- число объектов этой совокупности.
Понятие объема совокупности относится и к выборочной, и к генеральной совокупности.
Пусть из партии 100 пачек масла для исследования выбрано 10 пачек. Тогда объем генеральной совокупности $N=100$, а объем выборки $n=10$.
Исходя из первых двух определений, очевидно, что всегда выполняется неравенство $N>n$
Помимо этих двух совокупностей выделяют также репрезентативную или представительную выборку.
Репрезентативная (представительная) выборка -- выборка, в которой все объекты выбраны случайно и генеральной совокупности, то есть каждый объект генеральной совокупности имеет одинаковую вероятность попасть в выборку.
Выборка также может быть повторной и бесповторной.
Повторная выборка -- выборка, при которой выбранный объект возвращается обратно в генеральную совокупность перед выбором следующего объекта для исследования.
Бесповторная выборка -- выборка, при которой объект не возвращается обратно в генеральную совокупность перед выбором очередного объекта для исследования.
Способы отбора
Рассмотрим теперь различные способы отбора (схема 1).
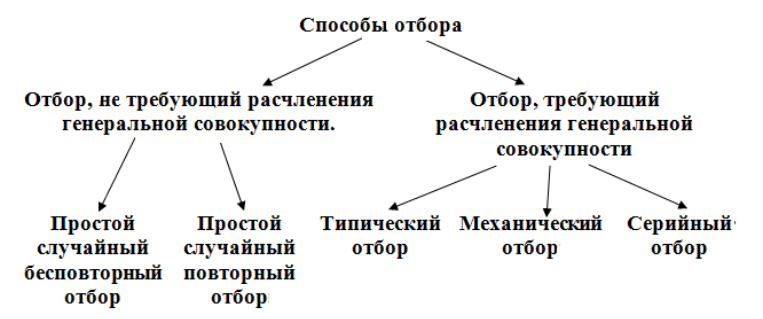
Рисунок 1. Способы отбора.
Разберемся теперь с каждым понятием по отдельности.
Простой случайный бесповторный отбор -- отбор, при котором объекты из генеральной совокупности выбираются по одному и не возвращаются обратно в генеральную совокупность.
Простой случайный повторный отбор -- отбор, при котором объекты из генеральной совокупности выбираются по одному и возвращаются обратно в генеральную совокупность.
Типический отбор -- отбор, при котором выборка производится не из всей генеральной совокупности, а из каждой его части по отдельности.
К примеру, если сметана произведена на трех разных заводах, то выборка делается по каждому заводу отдельно.
Механический отбор -- отбор, при котором генеральная совокупность делится на такое количество групп сколько объектов для исследования необходимо выбрать.
Пусть из партии 100 пачек масла нужно для исследования отобрать $10\%$. Тогда выбирается по одной пачке из каждых 10 пачек масла.
!!! Отметим, что при таком отборе выборка не всегда получается репрезентативной.
Серийный отбор -- отбор, при котором выборка происходит из генеральной совокупности не по одному, а сериями.
!!! На практике часто применяется комбинированный отбор, при котором используются сразу несколько видов отборов, перечисленных выше.
Формулы, связанные с понятием выборки
Введем несколько формул:
- Генеральная средняя при повторной выборке:
Отметим, что $\sum{N_i}=N$
- Генеральная средняя при бесповторной выборке:
- Выборочная средняя при повторной выборке:
Отметим, что $\sum{n_i}=n$
- Выборочная средняя при бесповторной выборке:
- Ошибка репрезентативности:
Пример задачи на нахождение ошибки репрезентативности
Пусть в магазине 20 видов глазированных сырков. Средняя цена 1 вида сырка составляет 10,4 рублей. Сырков с начинкой из этих видов составляет $25\%$ и средняя цена каждого вида с начинкой равняется 11 рублей. Найти ошибку репрезентативности данной выборки.
Решение:
Ошибка репрезентативности:
\[\triangle =\overline{x}-\overline{X}\]10,4 -- это генеральная средняя величина, то есть $\overline{X}=10,4$.
Так как сырки с начинкой составляют $25\%$, то сырков с начинкой$20\cdot 0,25=5$ видов.
Тогда выборочная средняя $\overline{x}=11$.
Получаем:
\[\triangle =\overline{x}-\overline{X}=11-10,4=0,6\]Ответ: 0,6.











