Основными понятиями теории вероятностей являются понятия события и вероятности события.
Событие
Событием будем называть любое утверждение, которое может как произойти, так и не произойти.
Обычно события обозначаются большими английскими буквами.
Пример: $A$ – выпадение числа $6$ на кости.
В связи с тем, что событие может иметь две вариации исхода («произошло» и «не произошло») мы сталкиваемся с понятие вероятности такого события.
Понятие вероятности события
Вероятностью события будем называть число, которое обозначает степень возможности, что такое событие произойдет.
Вероятность события обозначается как $P(A)$
Чтобы определить границы значения этого числа введем понятие достоверного и невозможного событий.
Достоверным событием будем называть такое, которое произойдет при любых обстоятельствах.
Примером такого события может быть следующее: Сумма «точек» на классической кости всегда равняется $21$.
Вероятность такого события мы будем принимать за единицу.
Невозможным событием будем называть такое, которое не может произойти ни при каком обстоятельстве.
Примером такого события может быть следующее: При игре в «очко» игрок набрал $1$ очко.
Вероятность такого события мы будем принимать за $0$.
То есть значение вероятности любого события содержится в отрезке $[0,1]$.
В современной теории вероятности принято выделять четыре определения для вероятности: классической, геометрическое, статистическое и аксиоматическое определения. Рассмотрим их отдельно.
Классическое определение
Классическое определение связано с такими неопределяемыми понятиями как равновозможность и элементарность события. Интуитивно их можно понять на следующих примерах:
Равновозможность: При подбрасывании монеты она может упасть как аверсом, так и реверсом независимо от внешних условий. То есть можно сказать что вероятность выпадения одной или другой стороны по сути одинакова.
Элементарность события: Если на кости выпадет число $4$, то это означает, что числа $1, 2, 3, 5$ и $6$ уже не выпали.
Вероятностью события будем называть отношения числа n равновозможных элементарных событий исходного события $B$ ко всем элементарным событиям $N$.
Математически это выглядит следующим образом:
$P(B)=\frac{n}{N}$
Геометрическое определение
Геометрическое определение применяется для случая, когда количество равновозможных событий будет бесконечно. Здесь, для введения геометрического определения рассмотрим следующий пример. Для игры дартс берем круг площадью $S$ и разбиваем его на несколько кругов. Какова вероятность, что дротик попадет в центральный круг? (Исключим здесь случаи полного непопадания в поле). Очевидно что равновозможных событий здесь будет бесконечно (как и общих событий) так как круг содержит в себе бесконечное число точек. Пусть площадь центрального круга равняется $s$. Тогда мы сталкиваемся с геометрическим определением вероятности такого события:
$P(B)=\frac{s}{S}$
Статистическое (частотное) определение
Классическое определение довольно часто не учитывает всех возможностей. Рассматривая даже классический пример с бросанием кости мы пренебрегаем возможностью, что не выпадет никакого из шести чисел (кубик просто «остановится» на уголке). Поэтому вводят следующее определение вероятности, учитывающее все возможности. Рассматриваем $N$ наблюдений. Пусть нужное нам событие при этом выпало $n$ раз. Тогда
$P(B)=lim_{N→∞}\frac{n}{N}$
Аксиоматическое определение
Данное определение задается с помощью аксиоматики Колмогорова.
Пусть $X$ - пространство всех элементарных событий. Тогда
Вероятностью события $B$ будем называть такую функцию $P(B)$, которая удовлетворяет следующим условиям:
- Данная функция всегда неотрицательна,
- Вероятность того, что произойдет хотя бы одно из попарно несовместных событий равняется сумме их вероятностей.
- Функция всегда меньше или равна $1$, причем $P(X)=1$.
Примеры задач
Найти вероятность того, что наугад вытащенная из колоды карт будет бубновой масти (сумма карт в колоде кратна $4$-м).
Решение.
Так как количество карт кратно четверке, то пусть всего карт будет $4k$. Тогда каждой масти карт будет $k$ штук (так как мастей $4$ и их количество одинаково).
При решении этой задачи будем использовать определение $5$. Во введенных нами обозначениях, получим что в определении $5$ мы будем иметь
$N=4k,n=k$
Следовательно
$P=\frac{k}{4k}=\frac{1}{4}$
Ответ: $\frac{1}{4}$.
Пусть нам дана точка $(a,b)$, где $-5
Решение.
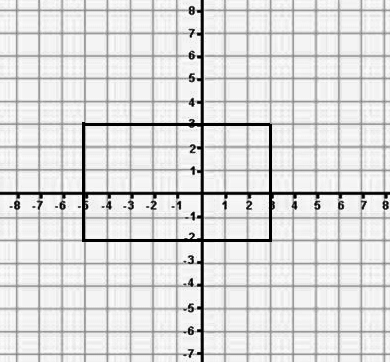
Тут мы будем использовать геометрическое определение. Изобразим вначале область, в которую в принципе может попасть эта точка (рис. 1).
Из этого рисунка видим, что
$S=8\cdot 5=40,s=3\cdot 3=9$
Тогда из геометрического определения:
$P=\frac{9}{40}$ Ответ: $\frac{9}{40}$.