В данной статье мы будем рассматривать понятие параллельного переноса в трехмерном пространстве. Но вначале нам надо рассмотреть такие понятия как отображение и движение в пространстве.
Понятие движения
Перед тем, как ввести понятие движения в пространстве, надо ввести определение отображения пространства на себя.
Отображением пространства на себя будем называть такое соответствие любой точке данного пространства какой-либо точке этого же пространства, в котором участвуют все точки из этого пространства.
Введем теперь, непосредственно, определение движения.
Движением пространства будем называть отображением пространства на себя, которое сохраняется расстояния между соответствующими точками.
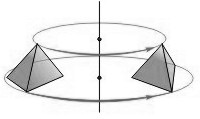
Пример – рисунок 1.
Введем теперь несколько теорем, связанных с понятием движения без доказательства.
При движении треугольник будет отображаться на равный ему же треугольник.
При движении пирамида будет отображаться на равную ей пирамиду.
Основными примерами движений в геометрии являются осевая симметрия, центральная симметрия, зеркальная симметрия, поворот и параллельный перенос. Доказательство того, что параллельный перенос действительно является движением, нами будет рассмотрено ниже.
Параллельный перенос
Введем теперь, непосредственно, понятие параллельного переноса на какой-либо вектор. Пусть нам дан вектор $\overline{α}$.
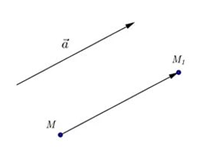
Параллельным переносом на вектор $\overline{α}$ будем называть такое отображение плоскости само на себя, при котором произвольная точка $M$ отображается на такую точку $M_1$, что выполняется равенство $\overline{MM_1}=\overline{α}$ (Рис. 2).
Введем следующую теорему, связанную с понятием параллельного переноса.
Параллельный перенос - движение.
Доказательство.
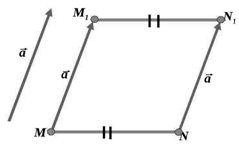
Рассмотрим в пространстве две произвольные точки $M$ и $N$. Будем рассматривать параллельный перенос на данный нам вектор $\overline{α}$. Пусть при нашем параллельном переносе данные нам точки отображаются, соответственно, в точки $M_1$ и $N_1$ (рис. 3).
Из определения 3 параллельного переноса получим, что $\overline{MM_1}=\overline{a}$, а $\overline{NN_1 }=\overline{a}$, следовательно, получим, что $\overline{MM_1}=\overline{NN_1}$.
Тогда, из определения равных векторов будем получать, что
$|MM_1|=|NN_1|$, $MM_1||NN_1$
Получаем, что четырехугольник $MM_1N_1N$ будет являться параллелограммом и, как следствие, верно равенство: $|MN|=|M_1N_1|$. Отсюда получаем, что параллельный перенос будет сохранять расстояния, что и доказывает нашу теорему.
Пример задачи
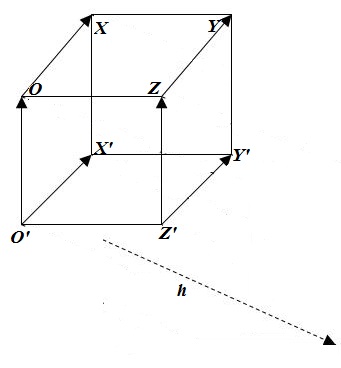
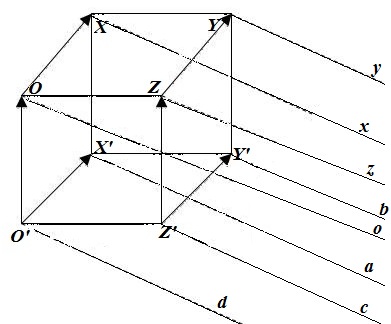
Постройте параллельный перенос куба на вектор $\overline{h}$, изображенных на рисунке 4.
Решение.
Для построения параллельного переноса сначала проведем через все точки тетраэдра прямые, параллельные заданному нам вектору $\overline{h}$ (рис. 5).
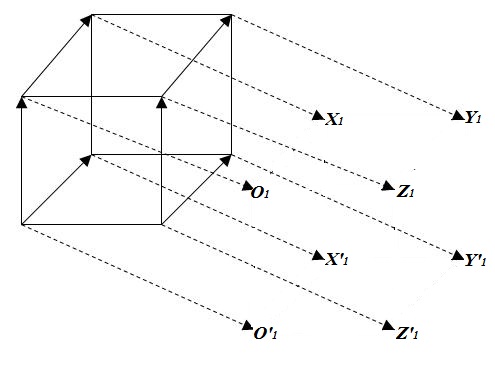
Далее, для построения будем использовать определение 3. Точка $X$ перейдет в такую точку $X_1$, которая будет принадлежать прямой $x$. Точка $Y$ перейдет в такую точку $Y_1$, которая будет принадлежать прямой $y$. Точка $Z$ перейдет в такую точку $Z_1$, которая будет принадлежать прямой $z$. Точка $O$ перейдет в такую точку $O_1$, которая будет принадлежать прямой $o$. Точка $X'$ перейдет в такую точку $X'_1$, которая будет принадлежать прямой $a$. Точка $Y'$ перейдет в такую точку $Y'_1$, которая будет принадлежать прямой $b$. Точка $Z'$ перейдет в такую точку $Z'_1$, которая будет принадлежать прямой $c$. Точка $O'$ перейдет в такую точку $O'_1$, которая будет принадлежать прямой $o'$. Причем будут выполняться равенства:
$\overline{XX_1}=\overline{h}$, $\overline{YY_1}=\overline{h}$, $\overline{ZZ_1}=\overline{h}$, $\overline{OO_1}=\overline{h}$, $\overline{X'X'_1}=\overline{h}$, $\overline{Y'Y'_1}=\overline{h}$, $\overline{Z'Z'_1}=\overline{h}$, $\overline{O'O'_1}=\overline{h}$
Отметим эти точки (рис. 6).
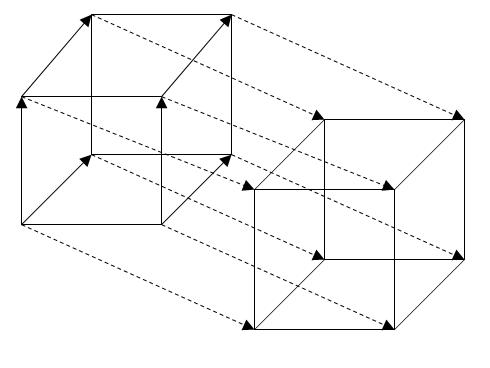
Соединив эти точки между собой, мы и получим искомый нами параллельный перенос на вектор $\overline{h}$ (рис. 7).