Понятие движения
Перед тем, как ввести понятие движения в пространстве, надо ввести определение отображения пространства на себя.
Отображением пространства на себя будем называть такое соответствие любой точке данного пространства какой-либо точке этого же пространства, в котором участвуют все точки из этого пространства.
Введем теперь, непосредственно, определение движения.
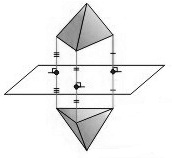
Движением пространства будем называть отображением пространства на себя, которое сохраняется расстояния между соответствующими точками.
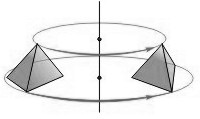
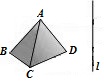
Пример – рисунок 1.
Введем теперь несколько теорем, связанных с понятием движения без доказательства.
При движении отрезок будет отображаться на ему же равный отрезок.
При движении треугольник будет отображаться на равный ему же треугольник.
При движении пирамида будет отображаться на равную ей пирамиду.
Основными примерами движений являются центральная, осевая и зеркальная симметрии. Рассмотрим их более подробно.
Центральная симметрия
Перед тем, как определить понятие центральной симметрии, введем понятие симметричности точки относительно другой точки.
Точки $X$ и $X_1$ будем называть симметричными относительно какой-либо точки $O$, если эта точка $O$ будет являться центром отрезка $[XX_1]$ (рис. 2).
Центральной симметрией фигуры относительно точки будем называть отображение, при котором получается фигура, составленная из точек, симметричных относительно данной точки каждой точке начальной фигуры.
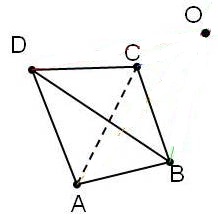
Постройте центральную симметрию тетраэдра, относительно точки $O$, изображенных на рисунке 3.
Решение.
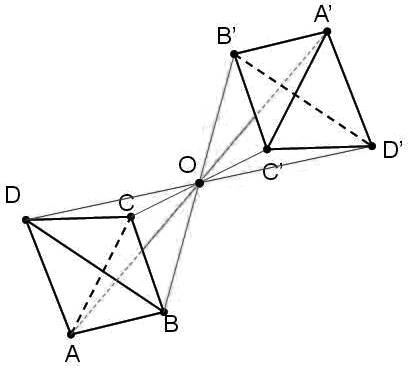
Для построения такой центральной симметрии сначала проведем через все точки тетраэдра прямые, каждая из которых будет проходить через точку $O$. На них построим отрезки, удовлетворяющие условиям
$|AO|=|A'O|$, $|BO|=|B'O|$, $|CO|=|C'O|$, $|DO|=|D'O|$
Таким образом, и получим искомую симметрию (рис. 4).
Осевая симметрия
Перед тем, как определить понятие осевой симметрии, введем понятие симметричности точки относительно какой-либо оси.
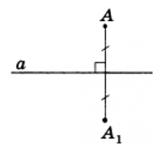
Точки$X$ и $X_1$ будем называть симметричными относительно какой-либо оси $a$, если прямая $(XX_1)$ будет перпендикулярна оси $a$ и при этом ось $a$ будет делить отрезок $[XX_1]$ пополам (рис. 5).
Осевой симметрией фигуры относительно оси будем называть отображение, при котором получается фигура, составленная из точек, симметричных относительно этой оси каждой точке начальной фигуры.
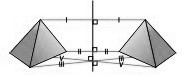
Постройте осевую симметрию тетраэдра, относительно оси $l$, изображенных на рисунке 6.
Решение.
Для построения такой осевой симметрии сначала проведем через все точки тетраэдра прямые, каждая из которых будет перпендикулярна к оси $l$. На них построим отрезки, для которых пересечение с осью $l$ будет центром. Соединив их концы, и получим искомую симметрию (рис. 7).
Зеркальная симметрия
Перед тем, как определить понятие зеркальной симметрии, введем понятие симметричности точки относительно какой-либо плоскости.
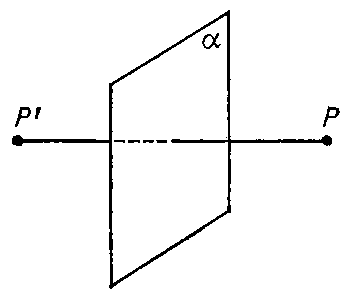
Точки $P$ и $P'$ будем называть симметричными относительно какой-либо плоскости $a$, если прямая $(PP')$ будет перпендикулярна плоскости $a$ и, при этом, плоскость $a$ будет делить отрезок $[PP']$ пополам (рис. 8).
Зеркальной симметрией фигуры относительно плоскости будем называть отображение, при котором получается фигура, составленная из точек, симметричных относительно этой плоскости каждой точке начальной фигуры.
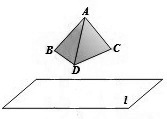
Постройте зеркальную симметрию тетраэдра, относительно плоскости $l$, изображенных на рисунке 9.
Решение.
Для построения такой симметрии сначала проведем через все точки тетраэдра прямые, каждая из которых будет перпендикулярна к плоскости $l$. На них построим отрезки, для которых пересечение с плоскостью $l$ будет центром. Соединив их концы, и получим искомую симметрию (рис. 10).