В древние времена люди для облегчения счета уже использовали различные средства и приборы. Изначально они для счета применяли пальцы на руках и ногах, затем использовали различные камушки, узелки на веревках, насечки на палках и т.д. Древние финикийские торговцы и вавилоняне использовали зерна или камешки, которые выкладывали на специальные доски. Позже стали использовать доски с камешками, на которых были углубления, по которым эти камешки передвигались. Подобное приспособление получило название абак и стало прародителем русских счетов.
Сегодня для облегчения процесса счета разработано большое количество разных приборов, среди которых одним из самых распространенных является микрокалькулятор.
Кроме вычислительных приборов используются измерительные приборы, которые также были изобретены в древние времена. Среди них самыми простыми и доступными является линейка и транспортир.
Микрокалькулятор
Прародителем микрокалькулятора является вавилонский абак. С возникновением необходимости производить более сложные расчеты стали разрабатываться более совершенные приборы для вычисления. Среди них были и вычислительные машины, над разработкой которых работали многие ученые на протяжении длительного времени, начиная с $XVII$ столетия.
Первые калькуляторы стали выпускаться в Англии в $1961$ г. Они по функциям напоминали современные электронные устройства. Первые карманные микрокалькуляторы были выпущены в $1971$ г.
С помощью микрокалькулятора можно выполнять арифметические действия – сложение, вычитание, умножение и деление. Калькулятор имеет табло, на котором высвечиваются цифры и результаты операций, и клавиатуру с клавишами цифр и арифметических действий.

Рисунок 1. Микрокалькулятор
Чертежный треугольник
В повседневной жизни человек постоянно встречается с понятием угол. Множество объектов содержит углы – тетрадь, книга, стол, комната, здание. Некоторые геометрические фигуры также содержат углы.
Изучение свойств углов началось еще в древности с развитием строительства и астрономии. Древние ученые именно благодаря знаниям о некоторых свойствах углов могли с высокой точностью рассчитывать расстояния до некоторых небесных тел и определять траекторию движения планет.
Для построения углов используется чертежный треугольник, с помощью которого можно легко построить прямой угол.

Рисунок 2. Чертежный треугольник
Транспортир
Для измерения углов использовались специальные инструменты, первые из которых появились более $4$ тысяч лет назад в Древнем Вавилоне, где была разработана система мер для определения величины угла. Вавилоняне делили круг на $360$ равных частей. Одну такую часть принято было считать единицей измерения углов. Такие единицы измерения сегодня называются градусами.
Транспортир является самым простым и распространенным инструментом для измерения величины углов. Этот инструмент был изобретен еще в глубокой древности, но его современное название происходит от французского «transporter» – «переносить».
Рассмотрим особенности использования транспортира.
Шкала на транспортир нанесена на полуокружность, центр которой отмечен на нем черточкой. Штрихи шкалы транспортира делят полуокружность на $180$ одинаковых делений. Если провести лучи из центра полуокружности через эти штрихи, то они образуют $180$ углов, каждый из которых равен $1/180$ доле развернутого угла. Такие углы и называются градусами.

Рисунок 3. Транспортир
Градусы обозначают знаком $°$. Каждое деление шкалы транспортира равно $1°$. Кроме делений по $1°$, на транспортире есть еще деления по $5°$ и по $10°$.
Транспортир также применяют и для построения углов.
Логарифмическая линейка
Логарифмическая линейка (или счетная линейка) используется для выполнения математических операций, таких как умножение, деление чисел, возведение в степень (например, в квадрат или куб), вычисление квадратных и кубических корней, логарифмов, тригонометрических и гиперболических функций и других операций. С помощью логарифмической линейки можно возвести число в любую действительную степень и извлечь корень любой действительной степени.
Логарифмическую линейку до появления карманных калькуляторов чаще всего использовали инженеры. Она позволяет производить расчеты с точностью около $3$ значащих цифр.
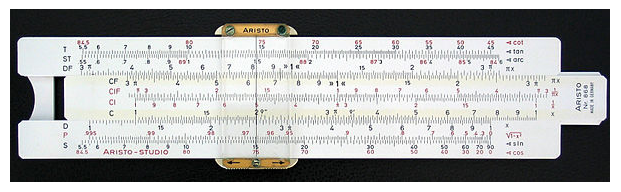
Рисунок 4. Логарифмическая линейка
Принцип действия логарифмической линейки состоит в том, что умножение и деление чисел заменено соответственно сложением и вычитанием их логарифмов.

Рисунок 5. Круговая логарифмическая линейка (логарифмический круг)
Самая простая логарифмическая линейка состоит из двух шкал, которые могут двигаться относительно друг друга. На обратной стороне линейки расположены справочные таблицы.
Например, для вычисления произведения двух чисел с помощью линейки нужно начало или конец подвижной шкалы совместить с первым множителем на неподвижной шкале, а на подвижной шкале найти второй множитель. Напротив него на неподвижной шкале будет результат умножения данных чисел.












