
Десятичная запись дробного числа
Дробное число можно представить в виде десятичной записи дробного числа.
Десятичная запись дробного числа представляет собой набор двух и более цифр от $0$ до $9$, между которыми находится так называемая \textit{десятичная запятая}.
Например, $35,02$; $100,7$; $123 \ 456,5$; $54,89$.
Крайняя левая цифра в десятичной записи числа не может быть нулем, исключением является только случай, когда десятичная запятая стоит сразу после первой цифры $0$.
Например, $0,357$; $0,064$.
Часто десятичную запятую заменяют десятичной точкой. Например, $35.02$; $100.7$; $123 \ 456.5$; $54.89$.
Определение десятичной дроби
Десятичные дроби -- это дробные числа, которые представлены в десятичной записи.
Например, $121,05$; $67,9$; $345,6700$.
Десятичные дроби используются для более компактной записи правильных обыкновенных дробей, знаменателями которых являются числа $10$, $100$, $1 \ 000$ и т.д. и смешанные числа, знаменателями дробной части которых являются числа $10$, $100$, $1 \ 000$ и т.д.
Например, обыкновенную дробь $\frac{8}{10}$ можно записать в виде десятичной дроби $0,8$, а смешанное число $405\frac{8}{100}$ -- в виде десятичной дроби $405,08$.
Чтение десятичных дробей
Десятичные дроби, которые соответствуют правильным обыкновенным дробям, читаются также как и обыкновенные дроби, только впереди добавляется фраза «ноль целых». Например, обыкновенной дроби $\frac{25}{100}$ (читается «двадцать пять сотых») отвечает десятичная дробь $0,25$ (читается «нуль целых двадцать пять сотых»).
Десятичные дроби, которые соответствуют смешанным числам, читаются также как и смешанные числа. Например, смешанному числу $43\frac{15}{1000}$ соответствует десятичная дробь $43,015$ (читается «сорок три целых пятнадцать тысячных»).
Разряды в десятичных дробях
В записи десятичной дроби значение каждой цифры зависит от ее позиции. Т.е. в десятичных дробях также имеет место понятие разряда.
Разряды в десятичных дробях до десятичной запятой называются так же, как и разряды в натуральных числах. Разряды в десятичных дробях после запятой вынесены в таблицу:
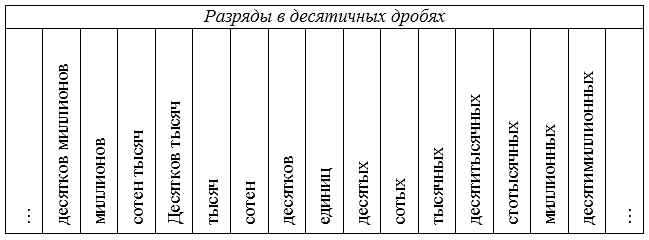
Рисунок 1.
Например, в десятичной дроби $56,328$ цифра $5$ стоит в разряде десятков, $6$ - в разряде единиц, $3$ - в разряде десятых, $2$ - в разряде сотых, $8$ -- в разряде тысячных.
Разряды в десятичных дробях различают по старшинству. При чтении десятичной дроби движутся слева направо -- от старшего разряда к младшему.
Например, в десятичной дроби $56,328$ старшим (высшим) разрядом является разряд десятков, а младшим (низшим) -- разряд тысячных.
Десятичную дробь можно разложить по разрядам аналогично разложению по разрядам натурального числа.
Например, разложим по разрядам десятичную дробь $37,851$:
$37,851=30+7+0,8+0,05+0,001$
Конечные десятичные дроби
Конечными десятичными дробями называют десятичные дроби, в записях которых содержится конечное число знаков (цифр).
Например, $0,138$; $5,34$; $56,123456$; $350 972,54$.
Любую конечную десятичную дробь можно перевести в обыкновенную дробь или смешанное число.
Например, конечной десятичной дроби $7,39$ отвечает дробное число $7\frac{39}{100}$, а конечной десятичной дроби $0,5$ соответствует правильная обыкновенная дробь $\frac{5}{10}$ (или любая дробь, которая равна ей, например, $\frac{1}{2}$ или $\frac{10}{20}$.
Перевод обыкновенной дроби в десятичную дробь
Перевод обыкновенных дробей со знаменателями $10, 100, \dots$ в десятичные дроби
Перед переводом некоторых правильных обыкновенных дробей в десятичные их нужно предварительно «подготовить». Результатом такой подготовки должно быть одинаковое количество цифр в числителе и количество нулей в знаменателе.
Суть «предварительной подготовки» правильных обыкновенных дробей к переводу в десятичные дроби -- дописывание слева в числителе такого числа нулей, чтобы общее количество цифр стало равно числу нулей в знаменателе.
Например, подготовим обыкновенную дробь $\frac{43}{1000}$ к переводу в десятичную и получим $\frac{043}{1000}$. А обыкновенная дробь $\frac{83}{100}$ в подготовке не нуждается.
Сформулируем правило перевода правильной обыкновенной дроби со знаменателем $10$, или $100$, или $1 \ 000$, $\dots$ в десятичную дробь:
-
записать $0$;
-
после него поставить десятичную запятую;
-
записать число из числителя (вместе с дописанными нулями после подготовки, если она была нужна).
Перевести правильную обыкновенную дробь $\frac{23}{100}$ в десятичную.
Решение.
В знаменателе стоит число $100$, которое содержит $2$ два нуля. В числителе стоит число $23$, в записи которого $2$.цифры. значит, подготовку для этой дроби к переводу в десятичную проводить не нужно.
Запишем $0$, поставим десятичную запятую и запишем число $23$ из числителя. Получим десятичную дробь $0,23$.
Ответ: $0,23$.
Записать правильную дробь $\frac{351}{100000}$ в виде десятичной дроби.
Решение.
В числителе данной дроби $3$ цифры, а число нулей в знаменателе -- $5$, поэтому данную обыкновенную дробь нужно подготовить к переводу в десятичную. Для этого необходимо дописать $5-3=2$ нуля слева в числителе: $\frac{00351}{100000}$.
Теперь можем составить нужную десятичную дробь. Для этого запишем $0$, затем поставим запятую и запишем число из числителя. Получим десятичную дробь $0,00351$.
Ответ: $0,00351$.
Сформулируем правило перевода неправильных обыкновенных дробей со знаменателями $10$, $100$, $\dots$ в десятичные дроби:
-
записать число из числителя;
-
отделить десятичной запятой столько цифр справа, сколько нулей в знаменателе исходной дроби.
Перевести неправильную обыкновенную дробь $\frac{12756}{100}$ в десятичную дробь.
Решение.
Запишем число из числителя $12756$, затем отделим десятичной запятой $2$ цифры справа, т.к. в знаменателе исходной дроби $2$ нуля. Получим десятичную дробь $127,56$.
Ответ: $127,56$.











