Рассмотрим произвольное вероятностное пространство $(\Omega ,{\rm F},F(x))$, где $F(x)$ - функция распределения случайной величины $\xi =\varphi (\omega )$.
Математическим ожиданием случайной величины $\xi =\varphi (\omega )$ называется действительное число
$M\xi =\int \limits _{\omega \in \Omega }\varphi (\omega ) P(d\omega )$, (1)
Где
\[\int \limits _{\omega \in \Omega }P (d\omega )=1.\]Математическое ожидание существует, если существует интеграл в (1), который называется интегралом Лебега (для его существования достаточно задать случайную величину и меру Лебега).
Основной недостаток интеграла Лебега в том, что, в общем случае, непонятно как его вычислять. Однако тот факт, что он существует, позволяет получать формулы, которые, возможно, только так и можно записать. Поэтому при вычислении интеграла Лебега часто используется интуитивный подход.
Если случайная величина дискретна, то интеграл (14) сводится к сумме
$\int \limits _{\omega \in \Omega }\varphi (\omega ) P(d\omega )=\sum \limits _{\omega \in \Omega }\varphi (\omega ) P(\omega )$, ($\sum \limits _{\omega \in \Omega }P(\omega ) =1$), (2)
в предположении, что ряд сходится абсолютно. В противном случае говорят, что интеграл и, тем самым, математическое ожидание не существует.
Таким образом, если дискретная случайная величина $\xi$ задается рядом распределения, то ее математическое ожидание вычисляется по формуле
$M\xi =\sum \limits _{i=1}^{n}x_{i} \cdot p_{i} $ или $M\xi =\sum \limits _{i=1}^{\infty }x_{i} \cdot p_{i} $, (3)
соответственно, при условии, что числовой ряд в правой части второй формулы (дискретная случайная величина имеет счетное число значений) сходится.
Если вероятностная мера задается на действительной оси, то она определяется функцией распределения, непрерывна и
$\int \limits _{\omega \in \Omega }\varphi (\omega ) P(d\omega )=\int \limits _{x\in (a,b)}x dF_{\xi } (x)$, (4)
где $a\le b$, $a,b\in R$.
Пусть функция $F_{\xi } (x)$ дифференцируема (принято говорить абсолютна непрерывна), тогда, как следует из (13)
отсюда
$M\xi =\int \limits _{-\infty }^{+\infty }x\cdot \rho _{\xi } (x) dx$. (5)
Математическое ожидание существует, если несобственный интеграл правой части (5) сходится. Если несобственный интеграл правой части равенства (5) расходится, то случайная величина $\xi$ не имеет конечного математического ожидания.
Замечание. Формулы (1), (2), (4) в дальнейшем не используются, содержащаяся в них информация носит общетеоретический характер.
Свойства математического ожидания
Всегда считаем, что случайные величины $\xi$ и $\eta$ определены на одном и том же вероятностном пространстве.
-
$Mc=c$, если $c=const$.
-
$M(c\cdot \xi )=c\cdot M\xi $, если $c=const$.
-
$M(\xi \pm \eta )=M\xi \pm M\eta $ для любых случайных величин $\xi$, $\eta$.
Если математические ожидания $M\xi $, $M\eta $ существуют, то $M(\xi \pm \eta )$ существует.
- $M(\xi \cdot \eta )=M\xi \cdot M\eta $, если $\xi$, $\eta$ $-$ независимые случайные величины.
Если математические ожидания $M\xi $, $M\eta $ существуют, то $M(\xi \cdot \eta )$ существует.
Геометрически математическое ожидание численно равно абсциссе центра тяжести интеграла (5).
Применение на практике
Симметричная монета подбрасывается два раза, а симметричная игральная кость -- один раз. Найти среднее число выпавших очков, если выпадению «герба» соответствует $1$, а «решетки» -- $0$. Проверить свойства $3, 4$ математического ожидания.
Решение. Пространство элементарных событий при двукратном подбрасывании монеты состоит из четырех точек $\Omega _{M} =\{ (0,0),(0,1),(1,0),(1,1)\} $, а пространство элементарных событий при одном бросании кости состоит из шести точек $\Omega _{K} =\{ (1),(2),(3),(4),(5),(6)\} $. Пространство $\Omega =\Omega _{M} \cdot \Omega _{k}$ состоит из $4\cdot 6=24$ точек:
(1,0,0), ... , (6,0,0),
(1,0,1), ... , (6,0,1),
(1,1,0), ... , (6,1,0),
(1,1,1), ... , (6,1,1).
Учитывая симметричность монеты и кости, воспользуемся классическим подходом. Каждому из элементарных событий дадим вероятность $1/24$.
Пусть $\xi$ -- случайная величина, определяющая число $i$ выпадений герба, $i=0,1,2$, а $\eta$ -- выпадение грани с цифрой $k$, $k=1,2,3,4,5,6$. Считаем, что случайные величины $\xi$, $\eta$ - независимы (следовательно $p_{ik} =p_{i} \cdot p_{k} $). Составим таблицу 3 (рис.1), где в клетках находятся вероятности реализации пары $(\xi ,\eta )$.
Свойство 3. а) $M(\xi +\eta )=\sum \limits _{i=0}^{2}\sum \limits _{k=1}^{6}(x_{i} +y_{k} ) \cdot p_{ik} =\left((0+1)\cdot \frac{1}{24} \right. +$
\[+(0+2)\cdot \frac{1}{24} +(0+3)\cdot \frac{1}{24} +(0+4)\cdot \frac{1}{24} +(0+5)\cdot \frac{1}{24} +\left. (0+6)\cdot \frac{1}{24} \right)+\] \[+\left((1+1)\cdot \frac{2}{24} +(1+2)\cdot \frac{2}{24} +(1+3)\cdot \frac{2}{24} +\right. (1+4)\cdot \frac{2}{24} +(1+5)\cdot \frac{2}{24} +\] \[\left. +(1+6)\cdot \frac{2}{24} \right)+\left((2+1)\cdot \frac{1}{24} +(2+2)\cdot \frac{1}{24} +(2+3)\cdot \frac{1}{24} \right. +\] \[+(2+4)\cdot \frac{1}{24} +\left. (2+5)\cdot \frac{1}{24} +(2+6)\cdot \frac{1}{24} \right)=\frac{1}{24} \cdot (1+2+3+4+5+\] \[+6)+\frac{2}{24} \cdot (2+3+4+5+6+7)+\frac{1}{24} \cdot (3+4+5+6+7+8)=\] \[=\frac{21}{24} +\frac{2\cdot 27}{24} +\frac{33}{24} =\frac{108}{24} =4,5\](свойство 1 выполнено);
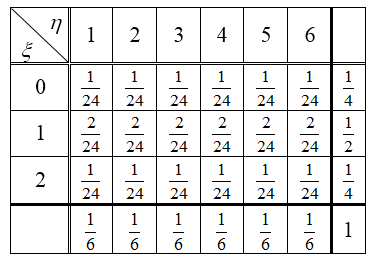
Рисунок 1.
б) $M\xi =0\cdot \frac{1}{4} +1\cdot \frac{1}{2} +2\cdot \frac{1}{4} =\frac{1}{2} +\frac{1}{2} =1>0$,
\[M\eta =1\cdot \frac{1}{6} +2\cdot \frac{1}{6} +3\cdot \frac{1}{6} +4\cdot \frac{1}{6} +5\cdot \frac{1}{6} +6\cdot \frac{1}{6} =\frac{21}{6} =\frac{7}{2} =3,5>0\](свойство 3 выполнено);
Свойство 4. а) $M(\xi \cdot \eta )=\sum \limits _{i=0}^{2}\sum \limits _{k=1}^{6}x_{i} \cdot y_{k} \cdot p_{ik} =\left(1\cdot 1\cdot \frac{2}{24} +1\cdot 2\cdot \frac{2}{24} \right. +$
\[+1\cdot 3\cdot \frac{2}{24} +1\cdot 4\cdot \frac{2}{24} +1\cdot 5\cdot \frac{2}{24} +\left. 1\cdot 6\cdot \frac{2}{24} \right)+\left(2\cdot 1\cdot \frac{1}{24} +2\cdot 2\cdot \frac{1}{24} +\right. \] \[+\left. +2\cdot 3\cdot \frac{1}{24} 2\cdot 4\cdot \frac{1}{24} +2\cdot 5\cdot \frac{1}{24} +2\cdot 6\cdot \frac{1}{24} \right)=\frac{2}{24} \cdot (1+2+3+4+\] \[+5+6)+\frac{1}{24} \cdot (2+4+6+8+10+12)=\frac{2\cdot 21}{24} +\frac{42}{24} =\frac{84}{24} =3,5,\]$M(\xi \cdot \eta )=M\xi \cdot M\eta =1\cdot 3,5=3,5$ (свойство 4 выполнено).












