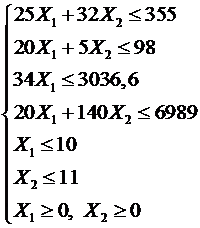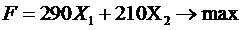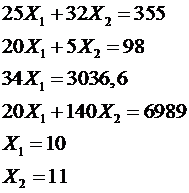Постановка и формализация задачи
Формирование производственной программы − важнейшая задача в системе планирования на предприятии. Программа производства разрабатывается на основе рыночных потребностей и с учетом возможностей предприятия.
Для оптимизации распределения объемов производства в условиях ограниченных ресурсов разрабатываются модели формирования производственной программы.
Постановка задачи определения оптимальной программы производства может выполняться различными методами: линейное программирование, метод множителей Лагранжа, динамического программирования, метод регрессионных моделей и др. Выбор метода зависит от математического вида целевой функции и ограничений.
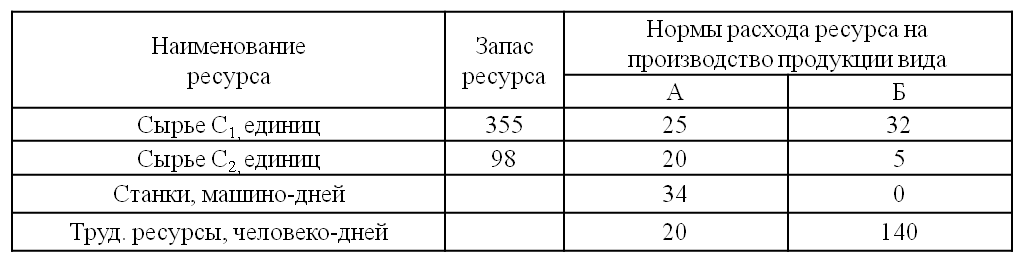
Пусть некое предприятие производит два вида продукции $A$ и $B$. Для этого используются следующие ресурсы: два вида сырья, 14 станков и 29 рабочих. Известны данные о запасах сырья, нормы расхода всех видов ресурсов на каждый вид продукции:
Прибыль от реализации единицы продукции $A$ составит 290 р., а от реализации единицы продукции $B$ составит 210 р. Коэффициент использования машинного времени – 0,9, коэффициент использования рабочего времени рабочих– 1, число рабочих дней в году − 241 день. Исследование рынка показало, что продукции вида $A$ можно реализовать в количестве не более 10 единиц, $B$ − не более 11 единиц.
Рассчитаем ресурс рабочего времени станков и рабочих:
- ресурс рабочего времени рабочих в нашем случае составит: $14\cdot 241\cdot 0,9 = 3036,6$ машино-дня;
- ресурс рабочего времени рабочих: $29\cdot 241\cdot 1 = 6989$ человеко-дней.
Составим математическую модель задачи. Пусть $X1$ – количество продукции вида $A$; $X2$ – количество продукции вида B. Запишем ограничения на запасы ресурсов и спрос:
Необходимо найти решение, которое при имеющихся ограничениях позволит максимизировать прибыль, то есть целевая функция будет записана как:
Построенная модель относится к классу задач линейного программирования, а так как число неизвестных параметров здесь равно двум, то она может быть решена графическим методом.
Решение задачи графическим методом
Графический метод решения задач линейного программирования характеризуется наглядностью и простотой.
Рассмотрим его алгоритм на нашем примере.
Построим на графике область допустимых решений (ОДР), для этого необходимо перейти от неравенств к равенствам и построить следующие линии:
Линия уровня целевой функции записывается следующим образом:
$290X1+210X2 = 0$
Это уравнения прямых линий, которые строятся по двум точкам:
- первое ограничение (ресурс $C1$): (0; 11,09), (14,2;0);
- второе ограничение (ресурс $C2%): (0; 19,6), (4,9; 0);C2%): (0; 19,6), (4,9; 0);
- третье ограничение (станки): (89,31; 0);
- четвертое ограничение (человеческие ресурсы): (0; 49,82), (349,45; 0);
- пятое ограничение (спрос на изделия А): (10; 0);
- шестое ограничение (спрос на изделия B): (0; 11);
- линия уровня целевой функции: (0;0), (1; - 1,38).
Построим данные линии в системе координат ($X1$ ; $X2$ ).
Перпендикулярно линии уровня целевой функции на графике строят градиент, то есть вектор, который характеризует направление и скорость изменения целевой функции.
ОДР на графике образована четырехугольником OAВС. Внутри него или на его границах ни одна точка не противоречит заданным ограничениям. Для нахождения оптимального решения необходимо перемещать линию уровня целевой функции в направлении градиента до крайней точки области допустимых решений.
В нашем случае такой точкой будет являться точка В с координатами: $X1=2,6; \ X2=9.$ При условии целочисленности решения оптимальная программа производства составит: 2 изделия $A$ и 9 изделий $B$. Прибыль предприятия в этом случае составит 2470 р.
По итогам решения задачи можно сделать вывод об узких местах и избыточных ресурсах. Так, на основе представленного графика видим, что объем производства ограничен запасами сырья, в то время как трудовой ресурс и машино-ресурс находятся в явном избытке.