Сложное высказывание
Высказывание является одним из ключевых понятий в логике. Точного определения, которое можно было бы использовать в равной мере во всех её разделах, нет. Но можно сказать, что это повествовательное предложение, в котором что-либо утверждается или отрицается. Кроме того, про любое высказывание можно сказать, истинно оно или ложно.
Высказывание будет считаться истинным, если то, что оно описывает соответствует реальной ситуации, и ложным, если описание не соответствует ей.
Из отдельных высказываний можно разными способами выстраивать новые высказывания. Так, из высказываний "Светит солнце" и "Дует ветер" можно образовать сложные высказывания "Светит солнце и дует ветер", "Либо светит солнце, либо дует ветер ", "Если светит солнце, то дует ветер" и т.п. Сложные высказывания образуются при помощи слов "и", "либо, либо", "если, то" и т.п., которые называются логическими связками.
Высказывание является простым, если в нём в качестве своих частей нет других высказываний.
Если высказывание с помощью логических связок получено из нескольких простых высказываний, то оно называется сложным.
В математической логике определены пять основных логических операций: инверсия, конъюнкция, дизъюнкция, импликация, эквивалентность. Три первые операции являются базовыми, составляют полную систему операций, т.е. остальные могут быть нормализованы (выражены через них). В информатике обычно используются именно эти три операции.
Способы построения базовых сложных высказываний
Отрицание (инверсия)
В русском языке этой логической связке соответствует частица НЕ (иногда нужно применить оборот «неверно что...»).
Отрицание — унарная (одноместная) операция; записывается в виде: $⌐A$ или $A^ ̅$. Например, отрицанием высказывания "$5$ – нечётное число" является высказывание "$5$ не есть нечётное число" (или: "Неверно, что $5$ есть нечётное число").
Если обозначить высказывание буквой $A$, а отрицание высказывания – символом "⌐", то понятие отрицания гласит: если высказывание $A$ истинно, его отрицание $⌐A$ ложно, и если $A$ ложно, его отрицание, $⌐A$, истинно. Например, высказывание "$4$ есть чётное число" истинно, а его отрицание "$4$ не является чётным числом" ложно, а так как "$4$ есть простое число" ложно, его отрицание "$4$ не есть простое число" истинно.
Отрицание (инверсию) можно представить в форме таблицы истинности, в которой "$1$" означает "истинно" и "$0$" – "ложно".
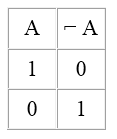
Рисунок 1.
Конъюнкция (логическое умножение)
Если соединить два простых высказывания при помощи связки "и" ("но", "а"), то получится сложное высказывание, которое называется конъюнкцией. Простые высказывания, которые соединяются таким способом, называются членами конъюнкции. Например, если высказывания "Вчера было солнечно" и "Сегодня тепло" соединить связкой "и", то получится конъюнкция "Вчера было солнечно и сегодня тепло ".
Конъюнкция истинна тогда и только тогда, когда все её составляющие являются истинными; в противном случае вся конъюнкция ложна.
Составляющее конъюнкцию высказывание $A$ может быть либо истинно, либо ложно, то же самое можно сказать и о высказывании $B$. Возможны четыре варианта комбинаций значений истинности для этих высказываний.
Если конъюнкцию обозначить символом "&", то таблица истинности для конъюнкции будет выглядеть следующим образом
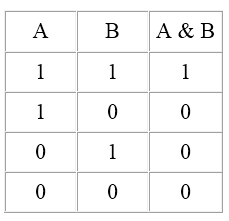
Рисунок 2.
Дизъюнкция
Для формальной логики совершенно не важен смысл простых высказываний. Достаточно знать, являются ли они истинными или ложными. Соединив два высказывания с помощью связки "или", можно получить логическое сложение (дизъюнкцию) этих высказываний. Простые высказывания, которые соединяются таким способом, называются членами дизъюнкции.
Слово "или" в обычном языке имеет два разных смысла. Оно может означать "одно или другое, или оба вместе", а может означать "одно или другое, но не оба вместе". Высказывание "Я хочу в этом сезоне пойти на "Волшебную флейту" или на "Ивана Сусанина" допускает возможность дважды посетить оперу. Высказывание "Он учится в Саратовском или в Московском университете" подразумевает, что студент учится только в одном из заявленных университетов.
В первом случае "или" называется неисключающим. Такая дизъюнкция двух высказываний истинна тогда, когда истинно хотя бы одно из этих высказываний. Во втором случае исключающая дизъюнкция двух высказываний истинна тогда, когда истинна только одна из её составляющих. Символом ∪ обозначим дизъюнкцию в неисключающем смысле, для исключающего "или" (дизъюнкции в исключающем смысле) будем использовать символ $Ủ$.
Таблица истинности для обоих видов дизъюнкции показывает, что неисключающая дизъюнкция истинна, тогда, когда истинна хотя бы одна из её составляющих; исключающая дизъюнкция истинна тогда, когда истинным является только один из ее членов, во всех остальных случаях она ложна.
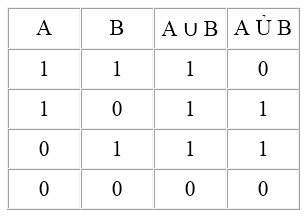
Рисунок 3.
Связка "или" в логике и математике всегда употребляется в неисключающем значении.
Импликация
Импликация – сложное высказывание, которое формулируется с помощью связки "если ..., то ..." и устанавливает, что одно событие, состояние и т.п. является в том или ином смысле основанием или условием для того, чтобы выполнилось другое. Например, сложное высказывание "Нет дыма без огня" состоит из двух простых высказываний "Есть огонь" и "Есть дым" и преобразуется в высказывание "Если есть огонь, то есть дым"; или "Если сумма цифр числа делится на $3$, то и само число делится на $3$" и т.п.
Условное высказывание состоит из двух простых высказываний. То, что стоит за словом "если", называется предпосылкой, основанием, условием, или антецедентом (предыдущим); высказывание, которое идёт после слова "то", называется следствием, выводом, или консеквентом (последующим).
Условное высказывание в логике называется импликацией.
Импликация истинна в трех случаях:
-
когда истинны и ее основание, и ее следствие;
-
когда условие ложно, а следствие истинно;
-
когда и предпосылка, и вывод ложны.
И только в одном случае, когда условие истинно, а следствие ложно, вся импликация ложна.
Обозначим импликацию символом $→$ и построим таблицу истинности для импликации:
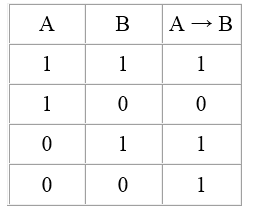
Рисунок 4.
Так, импликация ложна только в одном случае, когда из истинного основания следует ложный вывод.
Эквивалентность
Эквивалентность – сложное высказывание вида "$A$, если и только если $B$", она образуется из высказываний $A$ и $B$ и раскладывается на две импликации: "если $A$, то $B$" и "если $B$, то $A$". Например: "Четырёхугольник является квадратом, если и только если у него все стороны равны, и углы являются прямыми". Связка, с помощью которой из двух высказываний образуется сложное высказывание "..., если и только если ...", тоже обозначается "эквивалентность". При этом вместо "..., если и только если ..." могут использоваться "... тогда и только тогда, когда ...", "... в том и только том случае, когда ... " и т.п. Если обозначить эквивалентность символом $↔$, то для формулы $A ↔ B$ таблица истинности будет выглядеть следующим образом:
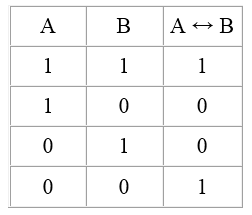
Рисунок 5.
Эквивалентность истинна тогда и только тогда, когда все составляющие ее высказывания либо ложны, либо истинны. Соответственно, эквивалентность является ложной, когда одно из входящих в нее высказываний истинно, а другое ложно.











