Основные приемы и методы решения логических задач
Рассмотрим разные способы решения логических задач.
Каждый из приемов имеет свою область применения.
Логические (или нечисловые задачи) относятся к нестандартным задачам. К ним относят текстовые задачи, в которых необходимо распознать объекты или расположить их в определенном порядке. При этом часть утверждений в условии задачи может быть истинной или ложной. К логическим задачам относят также задачи на переливания и взвешивания (фальшивые монеты и т.п.).
Можно выделить несколько различных способов решения логических задач, которые можно назвать следующим образом:
-
метод рассуждений;
-
метод таблиц;
-
метод графов;
-
метод блок-схем;
-
метод бильярда;
-
метод кругов Эйлера.
Метод рассуждений
Метод рассуждений является самым примитивным способом и его обычно применяют для решения самых простых логических задач. Идея метода заключается в проведении рассуждений при последовательном использовании всех условий задачи, вследствие чего приходят к выводу, который является ответом задачи.
Владимир, Семен и Олег изучают разные иностранные языки: английский, французский и немецкий. На вопрос, какой язык изучает каждый из них, один ответил: "Владимир изучает английский, Семен не изучает английский, а Олег не изучает немецкий". Впоследствии выяснилось, что в этом ответе только одно утверждение верно, а два других ложны. Какой язык изучает каждый из студентов?
Решение:
Имеем три утверждения. Если принять за истину первое утверждение, то правдиво и второе, т.к. студенты изучают разные языки, что противоречит условию задачи. Таким образом первое утверждение ложно.
Если правдивым является второе утверждение, то первое и третье должны быть ложными. В таком случае получаем, что никто не изучает английский. Это противоречит условию, таким образом, второе утверждение также является ложным.
Остается третье утверждение, которое можем считать верным, а первое и второе -- ложными. Таким образом, Владимир не изучает английский, его изучает Семен.
Ответ: Семен изучает английский язык, Олег -- французский, Владимир -- немецкий.
Метод таблиц
Основным приемом для решения текстовых логических задач является метод таблиц. С помощью таблиц можно наглядно представить условие задачи или ее ответ, кроме того их использование значительно помогают в принятии правильных логических решений.
У трех кукол Маши, Даши и Алены были платья трех разных цветов: красного, зеленого и синего. Туфли у них были таких же цветов. У Маши цвет платья и туфель совпадали. У Алены ни туфли, ни платье не были красными. Даша была в зеленых туфлях и в платье другого цвета. Как были одеты куклы?
Решение:
Составим таблицу, в которой отметим возможные цвета платьев и туфель кукол. По условию задачи заполним таблицу:
-
туфли Даши зеленые, а платье не зеленое. Следовательно, у Маши и Алены туфли уже не могут быть зелеными, так же как не могут быть туфли Даши синими или красными. Отмечаем все в таблице:
-
туфли и платье Алены не являются красными. Из таблицы видим, что красные туфли могут быть только у Маши, а, следовательно, туфли Алены -- синие. Правая часть таблицы заполнена.

Рисунок 1.
- Цвет платья Маши совпадает с цветом ее туфель, значит оно красное. Теперь легко увидеть, что у Алены -- зеленое платье, а у Даши -- синее.
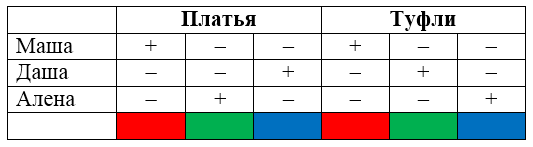
Рисунок 2.
Таблица полностью заполнена и в ней однозначно установлены цвета туфель и платьев кукол.
Ответ: Маша одета в красное платье и красные туфли, Даша в синем платье и зеленых туфлях, Алена в зеленом платье и синих туфлях.
Метод блок-схем
Этим методом решаются задачи, в которых с помощью сосудов требуется отмерить необходимое количество жидкости или связанные со взвешиванием на чашечных весах. Простейшим приемом решения таких задач является перебор всех возможных вариантов, который не является удобным и не дает возможности выделения общего подхода к решению подобных задач.
Суть метода блок-схем состоит в следующем:
-
выделяют операции для точного отмеривания жидкости, которые называются командами;
-
устанавливают последовательность выполнения команд, которая оформляется в виде блок-схемы (как в программировании). Составленная блок-схема является программой, выполнение которой должно привести к решению задачи, в ходе которой достаточно отмечать получаемые количества жидкости.
При выполнении программы удобно заполнять отдельную таблицу, в которую заносится количество жидкости в каждом из имеющихся сосудов.
Метод математического бильярда
Игра в бильярд стала предметом серьезных научных исследований в области механики и математики. Если представить горизонтальный бильярдный стол произвольной формы без луз, по которому без трения будет двигаться точечный шар, абсолютно упруго отражаясь от бортов стола, то возникал вопрос: какой может быть траектория этого шарика. В поисках ответа на этот вопрос появилась теория математического бильярда (теория траекторий).
С помощью данного метода можно очень легко решать задачи на переливание жидкостей.
Дано два сосуда -- объемом $3$ л и $5$ л. С помощью этих сосудов необходимо получить $1$, $2$, $3$, $4$, $5$, $6$, $7$ и $8$ литров воды. Имеется водопроводный кран и раковина, в которую можно выливать воду.
Решение:
Построим для данной задачи параллелограмм со сторонами $3$ и $5$ единиц. По горизонтали будет откладываться количество воды в литрах в пятилитровом сосуде, а по вертикали -- в трехлитровом. На всем параллелограмме нанесем сетку из одинаковых равносторонних треугольников:
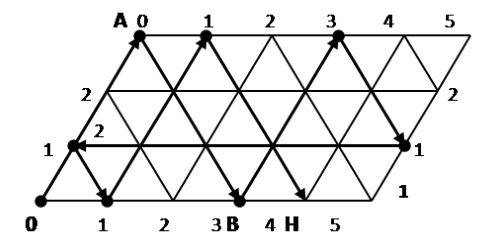
Рисунок 3.
Бильярдный шар может перемещаться только вдоль прямых, которые образуют сетку на параллелограмме. При ударе о сторону параллелограмма шар отражается и движется вдоль борта. При этом каждая точка соударения о сторону параллелограмма полностью характеризует, сколько воды находится в каждом из сосудов.











