Процесс возникновения диполя
В процессе образования ковалентной полярной связи один из атомов сильнее притягивает к себе электроны, в результате чего общая электронная пара смещается к его ядру. Возникает ковалентная полярная связь. Способность атома притягивать электроны является критерием его электроотрицательности (ЭО). Чем выше электроотрицательность у атома, тем больше вероятность смещения электронной пары в сторону ядра данного атома. Разность ЭО атомов характеризует полярность связи.
В результате смещения электронной пары к ядру одного из атомов, повышается плотность отрицательного заряда у данного атома и он получает эффективный заряд атома $\delta ^-$. У другого атома увеличивается плотность положительного заряда $\delta ^+$. Возникает диполь -- электрически нейтральная система с двумя одинаковыми по величине, но разными по знаку зарядами, находящимися на определенном расстоянии (длина диполя $l_д$) друг от друга.
Постоянный дипольный момент
Мерой полярности является дипольный момент $\mu $. Его величина равна произведению эффективного заряда $\delta $ на длину диполя $l_д$:
Единица измерения постоянного дипольного момента - кулон на метр ($Кл \cdot м$), или внесистемная единица измерения - дебай $D$, равная $3,34 \cdot 10-30 Кл \cdot м$.
Предположим, что в молекуле фтороводорода $HF$ - ионная связь. То есть на атомах водорода и фтора сосредоточены заряды $+1$ и $-1$, соответственно. Заряды ионов кратны заряду электрона, равному $1,60 \cdot 10^{-19}$ Кл. Расстояние между зарядами составляет $9,17\cdot 10^{-11}$ м. Постоянный дипольный момент, исходя из этих данных, равен:
$\mu = q \cdot r =1,60 \cdot 10^{-19} Кл \cdot 9,17 \cdot 10^{-11} м = 1,47 \cdot 10{-29} Кл \cdot м$.
В дебаях дипольный момент равен:
$\mu = \frac{1,47 \cdot 10^{-29} Кл \cdot м}{3,34 \cdot 10^{-30} Кл \cdot м \cdot D^{-1}} = 4,40 D$.
Величина $\mu = 4,40 D$ характеризует дипольный момент молекулы $HF$ при условии, что химическая связь в ней полностью ионная. В действительности же $\mu = 1,83 D$. Сопоставляя эти величины, можно вычислить «долю ионности связи» (частичный ионный характер связи) в молекуле $HF$.
Ионный характер связи = $\frac{1,83\ D \cdot 100}{4,40\ D}\ = 41,6\%$
С увеличением разности электроотрицательности постоянный момент диполя растет.
Дипольный момент является векторной величиной. Направление диполя условно принимают от отрицательного полюса к положительному.
У молекул аммиака $NH_3$ и фторида азота $NF_3$ одинаковая тригонально -- пирамидальная форма (Рис. 1). Полярность связей $N-H$ и $N-F$ тоже примерно одинакова. Однако дипольный момент аммиака равен $0,49 \cdot 10^{-29} Кл \cdot м$, а фторида азота - $0,07 \cdot 10^{-29} Кл \cdot м$. Такая разница объясняется тем, что в молекуле аммиака направление дипольного момента связывающей $N-H$ и несвязывающей электронной пары совпадает и при векторном сложении обусловливает больший электрический момент диполя. В молекуле фторида азота дипольные моменты связей $N-F$ и электронной пары направлены в противоположные стороны. Если их сложить, то происходит частичная компенсация.
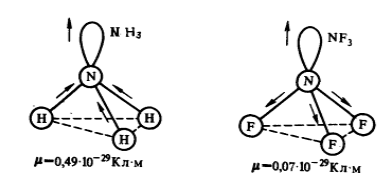
Рисунок 1. Направления дипольных моментов и электронных пар в молекулах аммиака $NH_3$ и фторида азота $NF_3$
Для многоатомных молекул необходимо различать дипольный момент отдельных связей и молекулы в целом. Если в молекуле присутствует несколько связей, то их электрические моменты (векторы) складываются по правилу параллелограмма. Результирующий дипольный момент будет отличаться от электрических дипольных моментов отдельных связей. Если молекула высокосимметрична, то дипольный момент может быть равен нулю, в то время как отдельные связи обладают высокой полярностью.
Молекула диоксида углерода линейной формы неполярна ($\mu = 0$), в то время как каждая связь $C=O$ имеет значительный дипольный момент ($\mu = 8,9 \cdot 10^{-29} Кл \cdot м$). Это происходит в результате того, что равные по величине постоянные дипольные моменты связей направлены навстречу друг другу.
Чем более полярна молекула и значительнее смещены общие электронные пары к одному из атомов, тем больше значение постоянного дипольного момента.
Методы определения постоянного дипольного момента
Как правило, методы определения электрических дипольных моментов основаны на нахождении ориентационного эффекта полярных молекул в приложенном электрическом поле.
-
Методы микроволновой спектроскопии. Основаны на эффектах расщепления и сдвига спектральных линий в электрическом поле. Позволяет наиболее точно определить значение величины и направление вектора постоянного дипольного момента. К этим методам относят: метод Штарка, резонансный микроволновой метод, молекулярных пучков и др.
-
Методы, основанные на измерении диэлектрической проницаемости $\varepsilon$ вещества.
При разных температурах измеряется диэлектрическая проницаемость веществ. Если вещество поместить в электрическое поле, создаваемое конденсатором, то емкость конденсатора возрастет в ? раз, то есть
где $c_0$ и $c$ -- емкость конденсатора в вакууме и в среде вещества.
Энергия электрического поля в конденсаторе равна:
где $U$ -- энергия электрического поля в конденсаторе;
$c$ -- емкость конденсатора в среде вещества;
$V$ -- напряжение на обкладках конденсатора.
В среде вещества конденсатор имеет больший запас энергии, чем в вакууме. Это объясняется тем, что под действием электрического поля происходит ориентация диполей и деформация молекул вещества.
Постоянный дипольный момент находят с помощью уравнения Ланженева -- Дебая, которое связывает температурную зависимость диэлектрической проницаемости и дипольный момент:
где $M$ -- относительная молекулярная масса вещества;
$\rho $ -- плотность;
$N_a$- число Авогадро;
$k$ -- постоянная Больцмана, равная $\frac{R}{N_a}$;
$R$- универсальная газовая постоянная;
$\alpha $ -- деформационная поляризуемость.
Измерив $\varepsilon$ при двух температурах при помощи уравнения Ланжевена - Дебая можно определить деформационную поляризуемость и постоянный дипольный момент.
Зная значение дипольного момента, можно указать характер химической связи (ковалентная полярная или неполярная, ионная) и судить о геометрической структуре молекулы.











