Молекулы типа изображенных ниже, являются линейными $\pi$-системами и условно называются полиенами:
Рисунок 1.
Следует учесть, что если $n$ приобретает четное значения, то молекулы будут представлять собой стабильные нейтральные полиены. Если $n$ приобретает нечетное значения, то молекулы будут представлять собой неустойчивые катионы, радикалы или анионы.
Другими словами полнен, в котором $n$ - нечетное число, является свободным радикалом. Например, при $n=3$ мы имеем $CH_2=CH-CH_2$ - радикал аллил.
Таким элементам свойственно вступать в реакции по концевым атомам сопряженных цепочек, благодаря этому они могут вступать в реакции присоединения по $1,n$- положению, а также способны к циклоприсоединению, сигматропным перегруппировкам, циклизованию и т.д.
Энергетические уровни полиенов
Для определения длины и энергии двойной и единичной связей в зависимости от длины цепи, мы должны рассматривать полную энергию равновесного состояния, обусловленную подвижными электронами. Вследствие взаимодействия $\pi $-электронов меняется не только длина $\pi $- и $\sigma $-связeй в двойных связях, но также длина $\sigma $-связей в единичных связях. Поэтому полная энергия связей, обусловленная подвижными электронами, будет складываться из полной энергии связей $\pi $-электронов в двойных связях и из энергии, необходимой для смещения длин всех $\sigma $-связей между углеродными атомами в цепи.
В рассматриваемых сопряженных цепях имеется $n$ двойных связей и $n-1$ единичных связей длиной.
Расчетные методы не позволяют произвести расчет энергии. Поэтому обычно прибегают к полуэмпирическим методам. Сущность одного из таких методов заключается в том, что он исходит из известных свойств этана и этилена. Энергия, необходимая для разрыва связей в этих молекулах, известна, что можно использовать для расчета энергии единичной и двойной связей
С увеличением длины сопряженной цепи разница в длинах двойной и единичной связей постепенно уменьшается и при бесконечной цепи значения длин этих связей становятся промежуточными между значениями длин «чистой» двойной и «чистой» единичной связей.
Для получения численных результатов в качестве длины «чистой» единичной и двойной связей используются экспериментальные значения межъядерного расстояния атомов углерода в этане, $- 1,54 \ Å \ $ , и длины двойной связи в этилене, $1,33 \ Å \ $ соответственно связи.
Итак, вычисления длины связей сопряженных углеводородных цепей методом МО дают два типа связей; длина связи одного типа является более короткой, чем «чистая» двойная связь, а длина связи другого находится между «чистой» двойной и «чистой» одинарной связью; с увеличением длины сопряженной цепи, длина указанных связей стремится сравняться и в пределе, при бесконечно длинной цепи становится равной $1,38$ ангстрема.
Энергетические уровни полиенов расположены симметрично относительно уровня $E - a$.
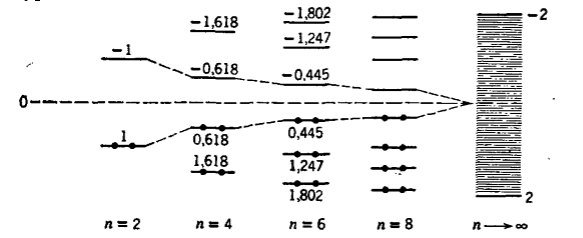
Рисунок 2.
Энергетические уровни полиенов, $n$-четное число
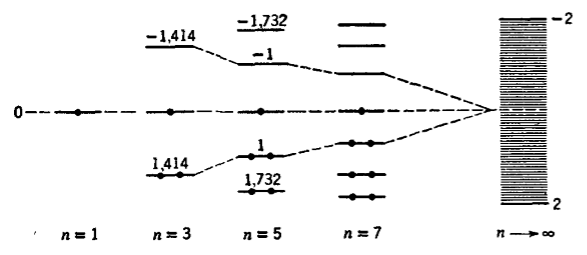
Рисунок 3.
Энергетические уровни полиенов, $n$-нечетное число
В основном состоянии молекул полиенов, как с четным, так и с нечетным числом атомов углерода в цепи электроны располагаются на низших энергетических уровнях. В полиенах с нечетным числом атомов на уровне $E = a$ имеется один неспаренный электрон. Этот существенный факт влияет на строение их систем.
Симметрия орбиталей в полиенах
В полиенах наблюдается чередование орбиталей по симметрии относительно проходящей через середину соединения зеркальной плоскости. При этом самая низкоэнергетическая орбиталь всегда будет симметричной.
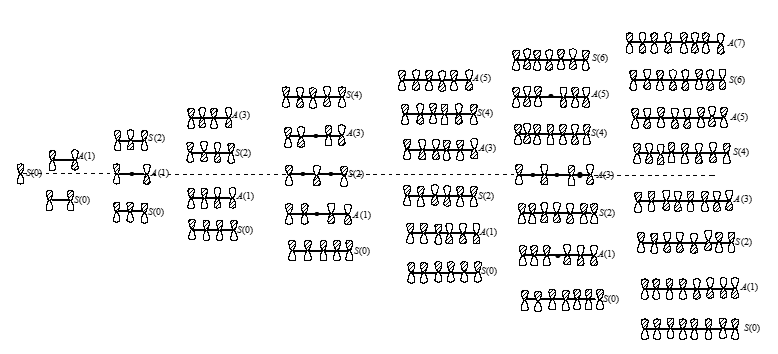
Рисунок 4. Узловые свойства и симметрия $\pi$-орбиталей полиенов. Буквами показаны симметричные (S) или антисимметричные (А) орбитали. Количество узлов указано в скобках.
Узловые свойства
Орбиталь которая является наиболее низкой по энергии не может иметь узлов. При переходе к более высокому, следующему уровню число узлов увеличивается на единицу
Узлы между каждыми соседними парами атомных орбиталей имеют высший уровень. Узлы всегда располагаются симметрично относительно центральной зеркальной плоскости.
Особенности нечетных полиенов
В полиеновых цепях с нечетным числом атомов центральный атом лежит в зеркальной плоскости, и антисимметричные орбитали должны иметь нулевой вклад от центрального атома. В этих случаях имеется несвязывающий уровень, в котором вклады четных атомов чередуются с $p$-орбиталями в альтернирующих фазах на нечетных атомах.
Вклады атомных орбиталей
Для каждой индивидуальной молекулярной орбитали сумма квадратов коэффициентов по всем составляющим ее атомным орбиталям равна единице. Для каждой индивидуальной атомной орбитали сумма $C2$ по всем молекулярным орбиталям, в которые она вносит вклад, тоже равна единице. Это обязательное требование для нормализованных (удовлетворяющих принципу квантования) орбиталей. Коэффициенты, характеризующие вклады отдельных атомов в каждую молекулярную орбиталь, можно вычислить по уравнению:
$Cij=[2/(N+1)]1/2sin[ij$\pi$/(N+1)]$,
$i$ - номер данной МО ($i=1$ для самой нижней молекулярной орбитали);
$j$ - положение данного атома в цепочке.
На рис. 4. приведены эскизы $\pi$-орбиталей для линейных полиенов с $n=1-8$, которые построены в соответствии с вышеперечисленными правилами, но без учета величины коэффициентов, характеризующих вклады отдельных атомов. Диаграмма правильно передает симметрию и узловые свойства $\pi$-орбиталей, и этого часто бывает достаточно для качественного предсказания реакционной способности молекул.












