Основным методом конструирования волновой функции МО является линейная комбинация атомных орбиталей (ЛКАО). Согласно методу ЛКАО-МО орбитали многоатомной молекулы (комплекса) можно представить в виде линейной комбинации орбиталей центрального атома и групповых орбиталей периферических атомов (лигандов).
От центрального атома в $\sigma $--взаимодействии в могут участвовать до шести орбиталей: $s$, $p_x$, $p_y$, $p_z$, $d_{x2-y2}$ и $d_{z2}$. Атомные (возможно -- гибридизованные) орбитали лигандов, подходящие по симметрии для $\sigma $--перекрывания вначале комбинируются. При этом получаются, так называемые, волновые функции групповых орбиталей $\Psi_L$:
$\Psi_L = c_1 \cdot \Psi_1 + c_2 \cdot \Psi_2 + c_3 \cdot \Psi_3 + c_4 \cdot \Psi_4 + c_5 \cdot \Psi_5 + c_6 \cdot \Psi_6$ ,
где $\Psi_i$ -- атомные орбитали лигандов; $c_i$ -- коэффициенты, отражающие вклад каждой орбитали в данную групповую орбиталь лигандов.
Затем готовят выражение для волновой функции, описывающей энергию взаимодействия определенной орбитали центрального атома (в ряде случаев они тоже гибридизуются, группируются) с данной групповой орбиталью лигандов:
$\Psi_{MO} = a \cdot \Psi_M \pm b \cdot \Psi_L$ ,
где $\Psi_M$ -- волновая функция атомной орбитали металла; $a$ и $b$ -- коэффициенты, отражающие вклад $\Psi_M$ и $\Psi_L$ в делокализованную (связывающую или разрыхляющую) молекулярную орбиталь комплекса.
Если какие-то орбитали или центрального атома или лигандов окажутся по соображениям симметрии неспособными комбинировать с орбиталями партнера, то они остаются неизменными, несвязывающими, как, например, орбитали $d_\varepsilon$ $(d_{xy}$, $d_{xz}$, $d_{yz})$ в октаэдрических комплексах без $\pi $--связывания.
Если в молекуле имеется центральный атом, то его атомные орбитали принадлежат к некоторому неприводимому представлению точечной группы данной молекулы. Для других атомов молекулы из подобных орбиталей специально образуют приведенные по симметрии линейные комбинации (ПСЛК). Эти новые орбитали пытаются комбинировать с АО центрального атома с целью получения МО.
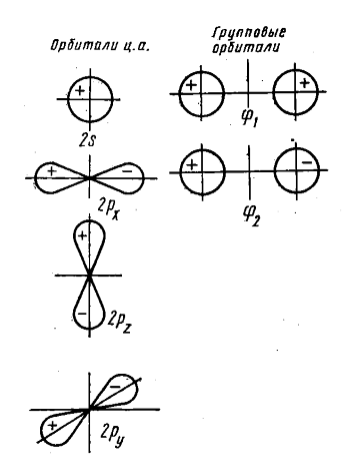
Рисунок 1. Орбитали центрального атома и отвечающие им по симметрии групповые орбитали периферических атомов линейной молекулы
Групповыми орбиталями называются орбитали ансамбля почти не связанных между собой атомов, имеющих определенное положение в пространстве. Термин «групповая орбиталь» связан с точечной группой симметрии данного ансамбля. Если рассматривается тетраэдрическое расположение атомов водорода в пространстве, то элементы симметрии групповых орбиталей являются элементами симметрии тетраэдра.
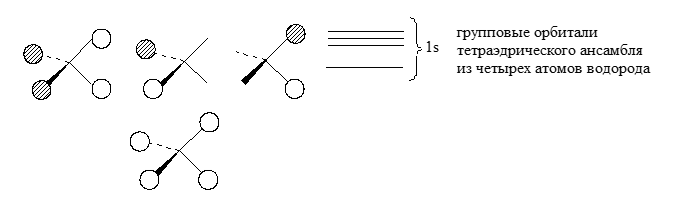
Рисунок 2.
Групповые орбитали молекулы $CO_2$
Форма молекулы $CO_2$ - линейная. На рис.2 показаны валентные орбитали центрального атома (углерода) и групповые орбитали лигандов (ГОЛ) - атомов кислорода.
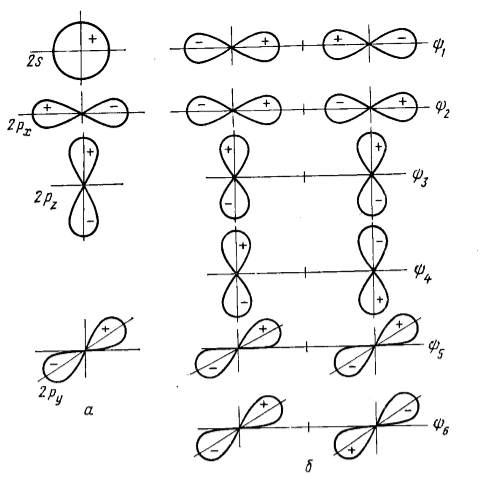
Рисунок 3. Орбитали центрального атома (а) и групповые орбитали (б) для трехцентровой линейной молекулы типа $CO_2$
Комбинации орбиталей центрального атома и групповых орбиталей
При построении молекулярных (т.е. делокализованных) $\sigma$-орбиталей многоатомных молекул используются орбитали фрагментов молекул. Например, из орбиталей фрагментов углеводородных фрагментов $CH$, $CH_2$ и $CH_3$ можно построить орбитали различных углеводородов. Орбитали фрагментов строятся на основе теории групп из так называемых групповых орбиталей ансамблей не связанных между собой атомов.
Групповые орбитали представляют собой сочетание двух орбиталей атомов водорода --- либо с одинаковыми знаками либо с разными знаками волновой функции $sp^2$ .
По условиям симметрии возможны следующие комбинации орбиталей центрального атома и групповых орбиталей (атомов водорода):
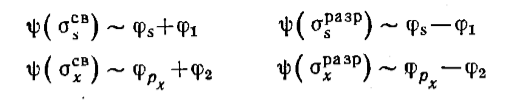
Рисунок 4.
Групповые молекулярные орбитали (МО) преобразуются по определенным типам симметрии для октаэдра. Предполагается, что от центрального иона в образовании связи участвуют $s-$, $p-$ и $d-$ орбитали, а от лигандов --- по одной $\sigma$- и две $\pi$-орбитали.

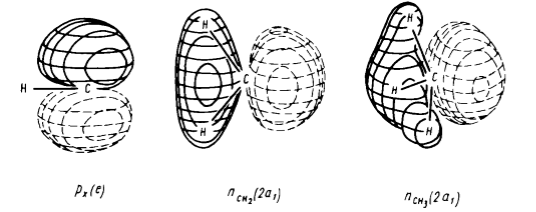
Рисунок 6. Трехмерное представление граничных МО групп $CH$, $CH_2$ и $CH_3$ полученных из неэмпирических расчетов












