Простейшим вариантом теории возмущений в методе молекулярных орбиталей (МО) является приближение граничных орбиталей, предложенное К.Фукуи в $1952$ г. Суть его состоит в допущении, что реакции легче всего протекают в случае максимального перекрывания граничных МО реагентов. Граничными считаются низшая вакантная и высшая заселенная молекулярные орбитали (НВМО и ВЗМО соответственно). Именно эти орбитали вносят максимальный вклад в энергию взаимодействия реагентов. При их перекрывании происходит перенос электронов с ВЗМО донора (нуклеофила) на НВМО акцептора (электрофила). Электронные переходы между НВМО и ВЗМО разрешены только в том случае, если орбитали одинаковы по симметрии и если переход не сопровождается изменением спина валентных электронов, но сопровождается изменением дипольного момента молекулы. Количеством орбиталей, между которыми разрешены электронные переходы, определяется число полос в электронных спектрах.
Основными характеристикам НВМО и ВЗМО являются их парциальные (граничные) электронные плотности, выражаемые через т.н. $индекс реакционной способности$. Мерой химической активности граничных орбиталей также может служить разница между ними по энергии.
Класссическим объектом применения приближения граничных орбиталей являются функциональные группы органических молекул, содержащие кратные связи. Такие группы весьма реакционноспособны, их принято называть $\pi $-реакционными центрами. Из рассмортения например, $\pi $-системы молекулы бутадиена (рис.1), которая представляется как «сконструированная» из двух винильных радикалов, можно определить, что разница по энергии между НВМО и ВЗМО для него ${\Delta Е_{\pi}}^{бут}$ составляет $545$ кДж/моль, в то время как для этилена эта разница ${\Delta Е_{\pi}}^{эт}$ составляет $670$ кДж/моль. Т.е. сопряжение двойных связей, характерное для бутадиена, приводит к сближению граничных орбиталей.
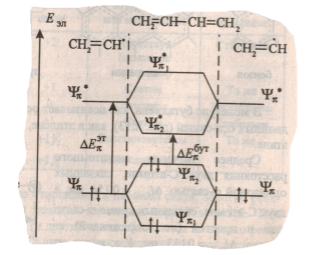
Рисунок 1. Энергетическая диаграмма $\pi $-орбиталей бутадиена
Энергии ВЗМО и НВМО могут меняться в результате межмолекулярных взаимодействий, например, растворителя и окрашенного растворенного вещества (хромофора). Это можно увидеть из анализа электронных спектров. В качестве примера можно рассматривать спектры $9$-флуорениллития ($9$-Фл-$Li^+$) в различных растворителях. В сильнополярном гексаметилфосфортриамиде (ГМФТА) происходит сольватация молекулы ($9$-Фл-$Li^+$) растворителем. Приводящая к ее электролитической диссоциации и пространственному расхождению катиона и аниона. За счет этого происходит делокализация электронной плотности аниона. При этом энергия ВЗМО растет, а энергия НЗМО понижается. Пик полосы поглощения смещается в длинноволновую область. И наоборот, в относительно слабополярном и слабосольватирующем 2,3-дигидропиране (ДГП) сохраняется тесный электростатический контакт между катионом и анионом, из которых состоит молекула ($9$-Фл-$Li^+$). При этом электронная плотность карбаниона «оттягивается» к месту контакта с противоионом $Li$, понижается энергия ВЗМО и повышается энергия НЗМО, а соответствующая им полоса поглощения хромофора смещается в коротковолновую область. Для 2,5-дигидрофурана и 3-метилгидрофурана, занимающих по сольватирующей способности промежуточное положение между ГМФТА и ДГП, наблюдается равновесие между диссоциированной и недиссоциированной формой ($9$-Фл-$Li^+$), что проявляется в наличии двух полос поглощения.
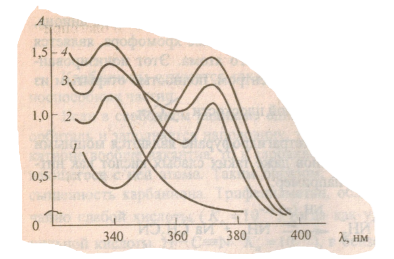
Рисунок 2. Влияние растворителей на электронный спектр 9-флуорениллития. 1 - гексаметилфосфортриамид; 2 - дигидропиран; 3 - дигидрофуран; 4 - метилтетрагидрофуран.
Приближение граничных орбиталей также использовали для объяснения реакций нитрования нафталина, диенового синтеза, нуклеофильного замещения второго порядка ($SN^2)$ (рис.3), при моделировании процесса фотосинтеза.
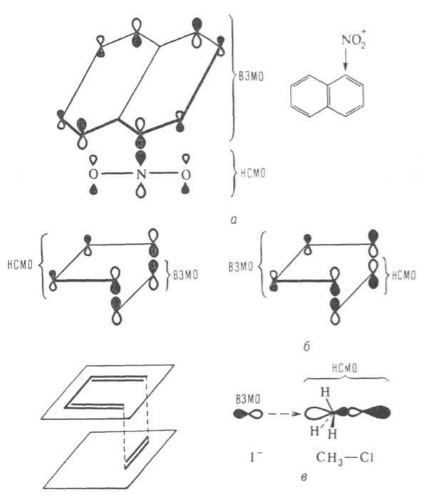
Рисунок 3. Орбитальные взаимодействия при нитровании нафталина (а), в диеновом синтезе (б) а также в реакции нуклеофильного замещения второго порядка $SN^2$(в)
В ряде случаев, например -- при протонировании пиридина, приближение граничных орбиталей неприменимо. Это объясняется тем, что в этом случае реакцию контролируют целые серии низколежащих заселенных и высоколежащих вакантных орбиталей. Поэтому, несмотря на удобство метода граничных орбиталей, его использование целесообразно только как первое приближение, которое должно уточняться с помощью более точных методов.
И, конечно же, не следует забывать, что ВЗМО и НВМО реагирующих молекул должны быть близки по энергии и обладать сходным типом симметрии.












