Симметрия и хиральность
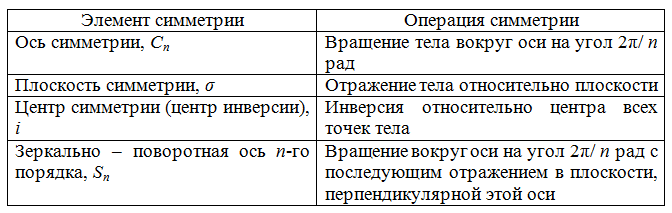
Свойства симметрии характеризуются операциями симметрии, которыми определяются элементы симметрии:
У молекул, в основном, можно наблюдать следующие элементы симметрии:
- оси вращения;
- зеркально – поворотные оси, выявляемые при рассмотрении операций симметрии.
-
Молекула обладает осью $C_n$, если ее структура полностью совпадает с исходным изображением при повороте вокруг оси на угол, равный $2\pi/ n$ рад.
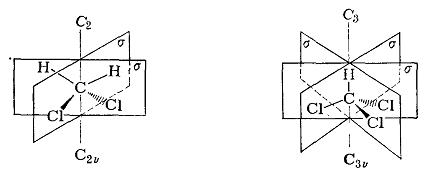
Например, молекула дихлорметана ($A$) имеет ось $C_2$, а молекула хлороформа (Б) – ось $C_3$
-
Молекула обладает осями $S_n$, если ее структура тождественна исходной только после поворота на угол $2\pi/ n$ рад и дальнейшего отражения в плоскости, ортогональной выбранной оси вращения.
Ось $S_1$ соответствует зеркальной плоскости симметрии $σ$ при $n=1.$
Например, у дихлорметана две $\sigma$-плоскости, у хлороформа – три.
Ось $S_2$ соответствует центру инверсии при $n=2$. Наличие центра инверсии указывает, что все лиганды в молекуле могут обращаться относительно центра.
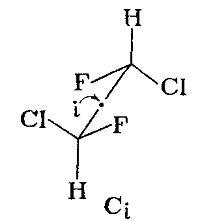
Пример 1Одна из конформаций в молекуле 1,2-дифтор-1,2-дихлорэтана имеет центр симметрии
Иногда можно встретить оси высшего порядка $S_n$, где $n$- четное число. Например, молекулы спиросоединений
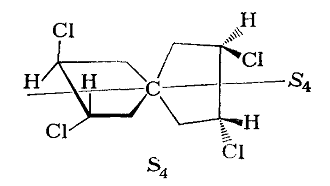
-
Если молекула содержит элементы симметрии типа Sn или оси высшего порядка $S_n$, то она обладает симметрией отражения и называется ахиральной или недиссимметричной. Такие молекулы не образуют энантиомерных пар.
- Молекулы, у которых отсутствует симметрия отражения, являются диссимметричными или хиральными.
- Хиральная молекула может быть симметричной при наличии осей $C_n (n > 1)$
Классификация молекул по точечным группам симметрии Ф.Коттона
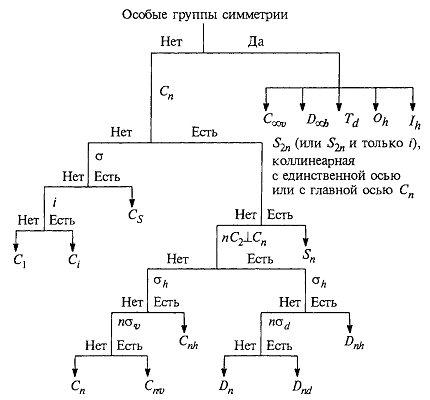
В 1971 году Ф. Коттоном предложена схема метода, позволяющая определить возможные элементы симметрии и классифицировать молекулы по точечным группам симметрии.
-
1Необходимо определить к какой «особой» группе принадлежит молекула: конус, цилиндр, икосаэдр, октаэдр, додекаэдр и др. $(C_∞v$ ,$D_∞h$ ,$O_h$ ,$I_h$ ,$T_d.)$
К группе $C_∞v$, $D_∞h$ могут принадлежать только линейные молекулы (ацетилен, хлорацетилен, дихлорацетилен).
-
Если ни к одной «особой» группе молекула не принадлежит, то ищут собственную ось вращение $C_n$.
В случае отсутствия собственной поворотной оси, ищут центр симметрии i, и тогда молекула принадлежит группе $C_i$, или зеркальную плоскость $\sigma$, в этом случае молекула принадлежит точечной группе $C_s$. При отсутствии элементов симметрии, кроме $E$, молекула относится к группе $C_1$.
-
Необходимо найти ось с наибольшим значением $n$, то есть главную ось $C_n$. Проверяем на наличие зеркально – поворотной оси $S_{2n}$, которая совпадала бы с главной осью.
Если ось $S_{2n}$ присутствует и других элементов (кроме $i$) нет, то молекула относится к одной из групп $S_n$ ($n$- четное число).
При наличии других элементов симметрии, кроме оси $S_{2n}$ (или при ее отсутствии) переходим к следующему действию.
-
В плоскости, перпендикулярной $C_n$, ищем группу из n осей второго порядка. Если такие оси есть, то молекула относится к одной из групп $D_n$, $D_{nh}$, $D_{nd}$. Если таких осей нет, то молекула принадлежит к группе $C_n$, $C_{nh}$, $C_{nv}$.
-
Молекула относится к группе $D_{nh}$, если у нее есть плоскость симметрии $\sigma h$, ортогональная главной оси. Если такой элемент отсутствует, то ищут набор из $n$ диагональных плоскостей $\sigma d$. $\sigma d$ – это такие плоскости симметрии, в которых расположена главная ось, но нет ни одной из перпендикулярных осей второго порядка.
В случае отсутствия и $\sigma d$ и $\sigma h$, молекула принадлежит группе $D_n$.
-
Если у молекулы есть плоскость $\sigma h$, то ее можно отнести к точечной группе $C_{nh}$. При отсутствии такой плоскости, ищут набор из $n$ плоскостей, которые проходят через главную ось.
Если такой набор плоскостей есть, то молекула относится к группе $C_{nv}$, если нет, то молекула относится к группе $C_n$.
Схематическое изображение алгоритма нахождения элементов симметрии