Связь между коэффициентами Бренстеда и значением $рKa$ катализатора
Каталитический закон Бренстеда можно сформулировать через взаимоотношения между свободной энергией реакции и свободной энергией активации каталитической стадии.
Первоначально считалось, что параметры $\alpha $ и $\beta $ являются мерой селективности реакции и их значения лежат в интервале от нуля до единицы.
Для реакций с участием кислородных кислот значения $\alpha $ и $\beta $ лежат в интервале $0-1,0$, а для карбокислот эти параметры находятся в пределах $0,42-0,89.$
При определении смысла коэффициентов $\alpha $ и $\beta $ были сделаны предположения:
-
Величина свободной энергии -- это линейная комбинация свободных энергий, связанных с заменой заместителя.
-
Переходное состояние, как по строению, так и по составу близко и к реагенту и продукту реакции. Изменение энергии Гиббса промежуточного состояния можно изобразить в виде линейного сочетания соответствующих изменений свободной энергии реагента и продукта реакции.
На основании этих допущений:
\[\delta G^{\ne }=a\delta {\overline{G}}^o_P+b\delta {\overline{G}}^o_R,\]где $\delta $ - оператор, описывающий эффект замены заместителя,
$G$ - свободная энергия Гиббса.
Несмотря на то, что стандартная энергия Гиббса переходного состояния соответствует максимальному значению на профиле потенциальной энергии, можно предположить, что изменение ее величины при замене заместителя будет промежуточным по сравнению с соответствующими изменениями энергии Гиббса реагента и продукта реакции.
где $0 \[\delta {\triangle G}^{\ne }=a\delta \triangle {\overline{G}}^o,\]
где ${\triangle G}^{\ne }={\overline{G}}^{\ne }-{\overline{G}}^o_R$ и $\triangle {\overline{G}}^о={\overline{G}}^o_P-{\overline{G}}^o_R$.
Коэффициент $\alpha $ (или $\beta $) является мерой сходства между промежуточным состоянием и реагентом или продуктом реакции. Увеличение значения $\alpha $ говорит о большем возрастании сходства с продуктом, чем с исходным веществом.
Однако, данное уравнение не всегда справедливо.
В своей основной форме соотношение $\delta {\triangle G}^{\ne }=\beta \delta \triangle {\overline{G}}^o$ является дифференциальным и его интегральные формы применимы в ограниченном диапазоне. Параметр $\beta $ является ограниченной константой, бренстедовские зависимости, при построении в широком диапазоне, могут быть нелинейными.
При замене одного субстрата другим допущение о постоянстве свободной энергии Гиббса в одной реакционной серии нарушится. Трансформация в исходном состоянии реакции сказывается на ее скорости.
Реакция разложения диазодигексилметана (Рис. 1). В качестве катализаторов использованы $19$ общих кислот со значениями $pK$, отличными на десять единиц. График бренстедовской зависимости сильно искривлен, каталитическая константа не зависит от силы кислоты при достижении значения $11 л/моль\cdot с$. При этом диффузионный предел составляет $10^9-10^{11} л/ моль\cdot с.$
Пунктирная кривая -- использовались только точки, соответствующие нейтральным кислотам, сплошная кривая -- точки, соответствующие карбоновым кислотам и фенолам
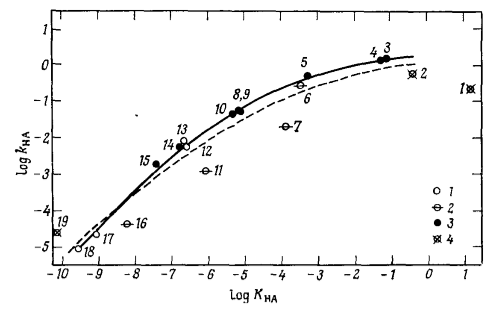
Рисунок 1. Бренстедовская зависимость для реакции разложения диазодигексилметана:1- фенолы; 2- нитрофенолы; 3- карбоновые кислоты; 4- другие кислоты.
Современные представления о механизме переноса протона
-
Диффузия $XH + Y ↔ XH\parallel Y$ (комплекс столкновения).
-
Перегруппировка $XH \parallel Y ↔ XH\cdot Y$ (реакционный комплекс).
-
Перенос протона $XH\cdot Y {{\stackrel{{\triangle G}^{\ne }}{\longleftrightarrow}}} X\cdot HY$ (реакционный комплекс).
-
Перегруппировка $X\cdot HY ↔ X\parallel HY$ (комплекс столкновения).
-
Диффузия $X\parallel HY ↔ X + HY$ (продукты).
Общий кислотный и общий основной катализ с медленным переносом протона
Перенос протона от $AH$ к $R$ и от $RH$ к $B$ -- самая медленная стадия всего многостадийного процесса.
Скорость реакции контролируется переносом протона от реагента $RH$ к катализатору $B_0$ (Рис. 2,а).
Энергетический профиль показан как наложение друг на друга параболических кривых потенциальной энергии для $RH$ и $B_0H^+$, которые соответствуют растяжению связи $R-H$ при переходе от $(RH+B_0)$ к состоянию $(R\dots H\dots B_0)$ и растяжению связи $B_0-H$ при переходе от $(B_0H^++R^-)$ к этому же переходному состоянию (Рис. 2,б).
Если изменить катализатор $B_0$ на более слабое основание $Bi$, то энергия сопряженной кислоты $BiH^+$ , будет несколько выше энергии $B_0H^+.$
В случаях, когда $Bi$ и $B_0$ сходны по типу и строению, форма кривых $BH^+$ будет одинакова. Одна из парабол будет сдвинута вертикально относительно другой без изменений (Рис. 2, в).
$Bi$ и $B_0$ представляют собой два замещенных в кольцо анилина.
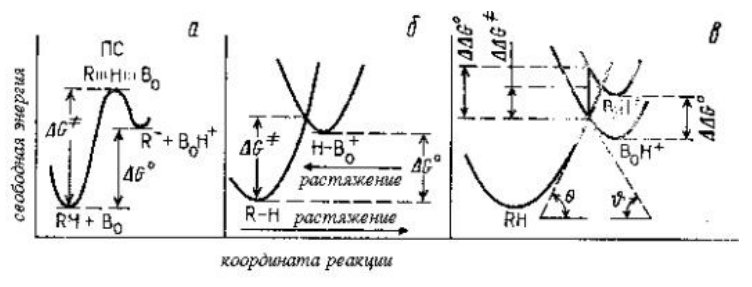
Рисунок 2. Реакция переноса протона (а), моделирование реакции переноса протона двумя кривыми растяжения связей (б), вывод соотношения Бренстеда (в)
Разность свободных энергий активации для реакций $RH+B_0$ и $RH+Bi$ будет пропорциональна разности свободных энергий Гиббса для равновесной диссоциации $RH+B_0^+$ и $RH+Bi^+.$
Величина коэффициента $\beta $ для основного катализа и величина $\alpha $ для кислотного катализа зависят от наклона кривых для $RH$ и $BH^+$ в точке их пересечения. При этом, параметры коэффициентов Бренстеда должны находиться в пределах от $0$ до $1$, то есть
для реакции $RH+B → R^- + BH^+ 0\le \beta \le 1$;
для реакции $R + AH → RH^+ + A^- 0\le \alpha \le 1$.
-
Если кривые пересекаются в вершине параболы $RH$, то $\beta =0$, тогда перенос протона происходит без затраты энергии.
-
Если скорость протона регулируется диффузией реагентов, то $\alpha → 0$, $\beta → 0$.
-
Если кривые пересекаются в вершине параболы $BH^+$, то $\beta=1$, тогда реагенты переходят в продукт в результате постепенного подъема по склону энергетической поверхности.
-
Для очень медленных процессов переноса протона $\alpha → 1$, $\beta → 1$ (реакции очень слабых кислот с очень слабыми основаниями).
Чаще всего в практике встречаются случаи, когда $0
Общий кислотный и общий основной катализ с быстрым переносом протона
Смысл коэффициентов Бренстеда для кислотно -- основных реакций с быстрым переносом протона будет иным, чем при медленном переносе протона.
Для общего кислотного катализа справедливы соотношения
$R + H_3O^+ {{\stackrel{K_1}{\Longleftrightarrow}}} RH^+ +H_2O$
$RH^+ +A^- {{\stackrel{k_2}{\longrightarrow}}} P + HA$
Применяя уравнение Бренстеда для основного катализа, получаем
В данном уравнении $K_1$ не зависит от природы катализатора и соотношение является уравнением Бренстеда для кислотного катализа с коэффициентом $\alpha =1-\beta $.












