
В отличие от атома водорода, для которого возможно точное решение уравнения Шредингера, для многоэлектронных атомов приходится пользоваться его приближенными решениями. При этом отсутствует вырождение электронов - их одинаковость по энергии в пределах одного значения главного квантового числа, и электроны, занимающие различные подуровни, отличаются друг от друга по энергии.
Заполнение электронных оболочек атомов определяется, главным образом, принципом Паули и правилом Хунда.
Принцип Паули
Принцип Паули состоит в следующем:
В атоме не может быть двух электронов в состояниях, характеризующихся 4-мя одинаковыми квантовыми числами.
Для построения электронных структур многоэлектронных атомов следует исходить из того, что в атоме будут заполняться все орбитали в порядке увеличения энергии электрона на каждой из них. Принцип Паули дает возможность рассчитать «емкость» электронных уровней и подуровней, которая оказывается равной числу соответствующих электронных состояний.
Если главное квантовое число $n=1$, то орбитальное и магнитное квантовые числа $l$ и $m_l$ имеют только одно значение - $0$. В этом случаеэлектроны могут различаться только спиновыми квантовыми числами. Т.о., для первого электронного слоя возможны 2 квантовых состояния, характеризующихся следующими наборами квантовых чисел: $n=1$, $l=0$, $m_l=0$, $s=+ \frac{1}{2}$ и $n=1$, $l=0$, $m_l=0$, $s=- \frac{1}{2}$. Т.к.для первого электронного слоя возможно только одно значение орбитального квантового числа, равное нулю, то оба электрона первого слоя будут s-электронами. Они находятся на s-орбитали шаровой симметрии. Эти элементы - водород и гелий. Электронная структура водорода записывается как $1s^1$, а гелия $1s^2$. В этих обозначениях первая цифра - главное квантовое число, «показатель степени» указывает число электронов орбитали данного типа. Таким образом, в атоме гелия первый электронный слой, содержащий $2$ электрона, заполнен целиком, что и является причиной химической инертности гелия.
Если $n=2$, то $l$ может принимать значения $0$ и $1$. Для $l=0$ можно записать $2$ комбинации квантовых чисел: $2$, $0$, $0$, $+ \frac{1}{2}$ и $2$, $0$, $0$, $- \frac{1}{2}$. Т.е. во втором электронном слое также могут находиться $2 s$-электрона. При $l=1$ магнитное квантовое число принимает уже $3$ значения: $+1$, $0$, $-1$ и возможны следующие комбинации квантовых чисел:

Рисунок 1.
При этом возможно нахождение на втором слое еще $6$ электронов. Это $р$-электроны, орбитали которых имеют гантелеобразную форму.
Итого, на втором электронном слое могут находиться $8$ электронов - $2 s$-электрона и $6 р$-электронов. Полностью заполненный второй слой можно записать в виде $2s^22p^6$.
Рассуждая аналогично, можно понять, что в $3$-ем слое может быть $18$ электронов ($3s^23p^63d^{10}$), а в четвертом - $32$ электрона ($4s^24p^64d^{10}4f^{14}$).
В основном состоянии атома электроны заполняют орбитали с самым низким уровнем энергии (рис.2.) Емкость первого слоя, как мы уже говорили, составляет $2$ электрона. Третий электрон, который появляется у атома лития $(Li)$, займет $2s$-подуровень; электронная структура лития - $1s^22s^1$
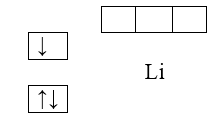
Рисунок 2.
Электронная структура бериллия $(Be)$ - $1s^22^2$; $2s$-подуровень заполнен целиком:
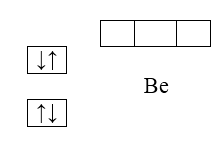
Рисунок 3.
Пятый электрон бора $(В)$ займет $2р$-подуровень, т.е. электронная труктура бора - $1s^22s^22р^1$
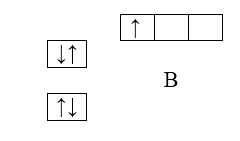
Рисунок 4.
Заполнение орбиталей подуровня. Правило Хунда
Порядок заполнения орбиталей подуровня определяется правилом Хунда:
В пределах подуровня электроны заполняют максимальное число орбиталей
Например. электронная схема атома углерода $(С)$ - $1s^22s^22р^2$. В соответствии с правилом Хунда, второй $р$-электрон займет пустую орбиталь, а не ту, на которой уже имеется электрон. Т.е. при построении электронной схемы он должен быть вписан в следующую пустую ячейку, а не в ту, в которой уже вписан предыдущий электрон:
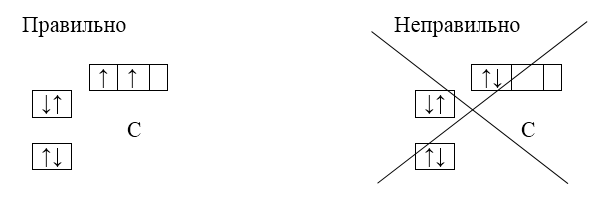
Рисунок 5.
В атоме азота $(N)$ все $2p$-орбитали оказываются занятыми:
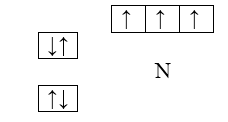
Рисунок 6.
Восьмой электрон кислорода $(О)$ помещается на уже занятую одним электроном $р$-орбиталь. Образуя пару электронов с противоположными спинами:
У фтора $(F)$ и неона $(Ne)$ расположение электронов на орбиталях атомов следующее:

Рисунок 7.
Если атом имеет несколько одиночных электронов, то спиновые моменты последних суммируются. Поэтому спины атомов $В$, $С$, $N$, $O$, $F$, $Ne$ равны соответственно $\frac{1}{2}$, $1$, $1 \frac{1}{2}$, $1$, $\frac{1}{2}$, $0$. С учетом этого правило Хунда можно сформулировать так:
Суммарный спин электронов в данном подуровне должен быть максимальным
Правило Клечковского
Иногда заполнение последующих электронных уровней начинается до того, как завершится заполнение предыдущих. Так, $4s$-электроны появляются в атомах, когда не заполнены еще $3d$-орбитали. Аналогичная картина наблюдается для $5s-$ и $4d-$, $6s-$ и $5d-$ электронов. Правило заполнения орбиталей было сформулировано В.М.Клечковским. Оно заключается в том, что заполнение орбиталей происходит в последовательности увеличения сумм главного и орбитального квантовых чисел $n + l = 1$, $2$, $3$ $...$ При каждом значении суммы $n + l$ заполнение орбиталей идет от больших $l$ и меньших $n$ к меньшим $l$ и большим $n$. Согласно этому принципу, заполнение электронами подуровней происходит в следующем порядке:
$1s → 2s → 2p → 3s → 3p → 4s → 3d → 4p → 5s → 4d → 5p → 6s → 4f → 5d → 6p → 7s → 5f → 6d$
Очевидно, что в соответствии с правилом Клечковского $19$-й электрон атома калия $(К)$ находится на $4s$-орбитали, т.е. его энергия меньше, чем если бы он находился на $3d$-орбитали. Однако в дальнейшем, начиная со скандия $(Sc)$, энергии электронов на $3d$-подуровне оказываются меньше, чем на $4s$-подуровне. Например, у атома титана $(Ti)$ сначала будут отрываться электроны с $4s-$, а затем - с $3d-$ подуровня.
Отклонения в строении слоев некоторых атомов в основном состоянии - хром $(Сr)$, медь $(Cu)$, молибден $(Mo)$, палладий $(Pd)$, серебро $(Ag)$, кадмий $(Сd)$, золото $(Au)$, - можно объяснить особой устойчивостью наполовину заполненных орбиталей подуровня. Так, у $d$-орбиталей устойчивыми являются $d^5$ и $d^{10}$, а у $f$-орбиталей - $f^7$ и $f^{14}$.










