Интерпретация физического смысла волновой функции

Определение физического смысла волновой функции

Чтобы знать, что «означает» волновое уравнение, необходимо установить, что «означает» волновая функция $\psi $. В волновом уравнении для атома водорода

${\mathcal H}\psi =\left[-\frac{{\hbar }^2}{8{\pi }^2m}\left(\frac{{\partial }^2}{\partial x^2}+\frac{{\partial }^2}{\partial y^2}+\frac{{\partial }^2}{\partial z^2}\right)-\frac{e^2}{r}\right]\psi =E\psi $ (1)

взяты вторые производные $\psi $ относительно координат электрона $x$, $y$ и $z$. Отсюда следует, что $\psi $ должна быть функцией трех координат. Функция $\psi (x, y, z)$ имеет определенное значение для некоторой данной комбинации значений $x$, $y$ и $z$, или, другими словами, $\psi $ имеет определенное значение в какой-либо точке пространства (если положение ядра атома водорода - протона принято за начало системы координат), определяемой координатами $x$, $y$ и $z$.

Физический смысл этой величины заключается в том, что она связана с вероятностью нахождения электрона в данной точке. Точная форма этой связи очень проста. Вероятность Р нахождения электрона в точке ($x$, $y$, $z$) равна:

$P=\psi \left(x,\ y,\ z\right){\psi }^*\left(x,\ y,\ z\right)$ (2)

где ${\psi }^*$ представляет собой комплексносопряженную функцию $\psi $; поскольку $\psi $ может иметь и мнимые значения, то, чтобы $Р$ была действительной величиной, функцию $\psi $ следует умножить на ее комплексносопряженную функцию. Вероятность нахождения электрона в какой-либо точке может быть большой или малой величиной или даже равной нулю, но, очевидно, не может быть мнимой. Конечно, если $\psi $ действительная величина, то $\psi*$ = $\psi $ и уравнение 2 просто свидетельствует о том, что вероятность равна $\psi^2$.

Из этого определения физического смысла значения $\psi $ следует, что любая такая функция должна удовлетворять перечисленным ниже требованиям:

1. Она должна иметь только одно значение в каждой точке, так как, какие бы ни были значения $x$, $y$ и $z$, должен быть лишь один определенный ответ на вопрос: «Какова вероятность того, что электрон находится в точке ($x$, $y$, $z$)?»

2. Она не должна иметь значение $\infty$ ни в одной из точек;

3. Ее абсолютные значения во всех точках должны быть такими, чтобы

$\int\limits^{+\infty }_{-\infty }{\int\limits^{+\infty }_{-\infty }{\int\limits^{+\infty }_{-\infty }{\psi \left(x,\ y,\ z\right){\psi }^*\left(x,\ y,\ z\right)dxdydz=\int{\psi {\psi }^*d\tau =1}}}}$ (3)

Левая часть уравнения 3 дает сумму вероятностей нахождения электрона в каждой точке по всему пространству. Так как имеется один электрон и он должен где-то находиться, общая вероятность поэтому должна быть равна единице. Средняя часть уравнения 3 представляет собой просто краткую форму записи левой части, в которой $d\tau $ означает элементарный объем: интегрирование, понятно, ведется по всем координатам. Когда волновая функция удовлетворяет условию 3, говорят, что она нормирована.

Способы представления волновой функции

Если уравнение 1 переписать в сферических полярных координатах $r$, $\theta $ и $\varphi $, которые связаны с декартовыми координатами $x$, $y$ и $z$ так, как показано на рис. 1, оно приобретает вид:

$\frac{1}{r^2}\frac{\partial }{\partial r}\left(r^2\frac{\partial \psi }{\partial r}\right)+\frac{1}{r^2sin\theta }\frac{\partial }{\partial \theta }\left(sin\theta \frac{\partial \psi }{\partial \theta }\right)+\frac{1}{r^2sin^2\theta }\frac{{\partial }^2\psi }{\partial {\varphi }^2}+\frac{8{\pi }^2m}{{\hbar }^2}\left(E+\frac{e^2}{r}\right)\psi =0$ (4)

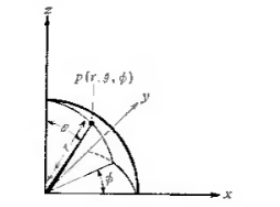
Рисунок 1. Система полярных координат

Это уравнение можно решить и получить набор волновых функций. Чтобы понять физический смысл $\psi $ детально исследуем одну из них, ту, которая соответствует наиболее низкой энергии $\psi $1 и имеет следующий вид:

${\psi }_1=\frac{exp\left(-{r}/{a_0}\right)}{\sqrt{\pi }a^{{3}/{2}}_0}$ (5)

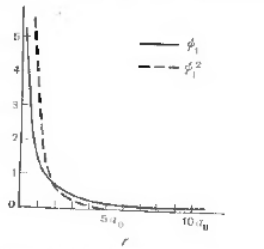
Рисунок 2. Графики волновых функций основного состояния атома водорода

Здесь $а_0$ означает боровский радиус, а $r$ - расстояние до ядра. На рисунке 2 приведен график, соответствующий функции $\psi $1, а также ${\psi }^2_1$. Следует отметить, что эти функции являются сферически симметричными, так как их значения не зависят от углов $\theta $ и $\varphi $. Функция $\psi $1 удовлетворяет ранее упомянутым требованиям и ее можно считать волновой в том смысле, что она: а) однозначна, б) никогда не является бесконечной и в) нормирована.

Другой способ представления данной функции показан на рисунке 3. Этот рисунок можно интерпретировать несколькими способами:

1. Прежде всего, представим себе, что имеем очень большое число атомов водорода. В некоторый момент времени электроны в каждом атоме в общем будут находиться на разном расстоянии от ядра. Если изображения всех этих атомов наложить друг на друга, то получим картину, представленную на рис. 3.

2. Можно взять только один атом и наблюдать его много раз, по мере того, как электрон будет менять свое положение относительно ядра. Если затенить каждую маленькую область пространства пропорционально тому, как часто находится в нем электрон, то получится картина, показанная на рис. 3.

3. Можно вообще отказаться от изображения электрона как крошечного твердого тела, движущегося вокруг протона, и вместо этого рассматривать его как некоторое количество отрицательного заряда и массы, которая распределена или размазана вокруг ядра в соответствии с уравнением 2. В этом случае рисунок 3 представляет собой, грубо говоря, то, что можно было бы «увидеть» если бы можно было посмотреть на атом.

Рисунок 3. Представление волновой функции основного состояния атома водорода

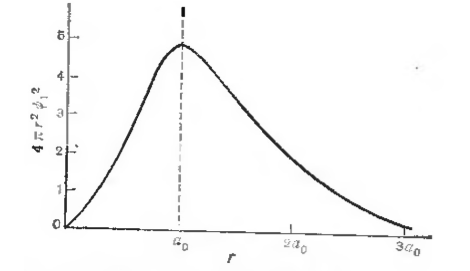
Посмотрим теперь, как можно квантовомеханическую картину основного состояния с размазанным электроном сопоставить с картиной, предложенной Бором. Предположим, что рассматриваемое пространство вокруг ядра разделено на бесконечное число бесконечно малых тонких концентрических сферических оболочек, и зададим вопрос, какова вероятность того, что электрон будет находиться в каждой из них. Общий объем такой оболочки толщиной $\Delta r$ равен $4\pi r^2\Delta r$, и общая вероятность нахождения электрона в этом объеме составляет ($4\pi r^2\Delta r)\ {\psi }^2_1$. На рис. 4. построен график зависимости величины $4\pi r^2\ {\psi }^2_1$ относительно $r$. Максимум кривой лежит при значении $r$, равном $а_0$. Эта величина называется радиусом Бора, так как это есть радиус орбиты боровского атома водорода, которой соответствует наименьшее количество энергии электрона. Таким образом, если модель Бора для атома водорода позволяет заключить, что в основном состоянии электрон всегда должен вращаться вокруг протона по круговому пути с радиусом, точно равным $а_0$, то волновая механика свидетельствует только о том, что это наиболее вероятный радиус.

плотности вероятности орбитали основного состояния атома водорода">

Рисунок 4. Функция плотности вероятности орбитали основного состояния атома водорода