Вектор напряжённости магнитного поля как вспомогательный вектор для описания поля в магнетиках
Когда мы рассматриваем магнитное поле в вакууме при отсутствии магнетиков, магнитное поле порождается токами проводимости и выполняется равенство:
где $\overrightarrow{j}$ -- вектор плотности токов проводимости.
В магнетиках поле возникает благодаря токам проводимости и молекулярным токам ($\overrightarrow{j_m}$), что необходимо учитывать. Для молекулярных токов имеет место векторное равенство:
где $\overrightarrow{j_m}$ -- объемная плотность молекулярных токов, $\overrightarrow{J\ }$ - вектор намагниченности. Так, при наличии магнетиков выражение (1) с учетом равенства (2) примет вид:
Выразим ток проводимости из уравнения (3), получим:
Определение вектора напряженности магнитного поля
Вектором напряженности магнитного поля называют вектор, равный:
Напряженность магнитного поля не является чисто полевой величиной, так как включает вектор $\overrightarrow{J\ },\ $который является характеристикой намагниченности среды. По своему значению $\overrightarrow{H}$ является вспомогательным вектором и играет роль подобную вектору электрического смещения $\overrightarrow{D\ }\ $в электричестве.
Основные уравнения для вектора напряженности
Из определения вектора $\overrightarrow{H}$ и уравнения (4), следует весьма удобное уравнение для вычисления поля в магнетиках:
Закон полного тока при наличии магнетиков имеет вид:
Формула (7) выражает теорему о циркуляции вектора напряженности магнитного поля, которая гласит:
«Циркуляция вектора напряженности магнитного поля по некоторому контуру равна алгебраической сумме макроскопических токов, которые охвачены заданным контуром».
В вакууме $\overrightarrow{J\ }=0$, тогда:
\[\overrightarrow{H}=\frac{\overrightarrow{B}}{{\mu }_0}\left(8\right).\]Напряженность поля прямолинейного бесконечного проводника в вакууме определяется формулой:
\[H=\frac{1}{2\pi }\frac{I}{b}\left(9\right),\]где $b$ -- расстояние от проводника до точки, где рассматривается поле. Из формулы (9) определяется размерность напряженности магнитного поля. Основная единица напряженности в системе СИ -- ампер деленный на метр ($\frac{А}{м}$).
Связь и вектора напряженности магнитного поля с намагниченностью и вектором магнитной индукции
Обычно вектор намагниченности ($\overrightarrow{J}$) связывают с вектором напряженности в каждой точке магнетика:
\[\overrightarrow{J}=\varkappa \overrightarrow{H}\left(10\right),\]где $\varkappa $ -- магнитная восприимчивость, безразмерная величина. Для неферромагнитных веществ и в не больших полях $\varkappa $ не зависит от напряженности. В анизотропных средах $\varkappa $ является тензором и направления $\overrightarrow{J}$ и $\overrightarrow{H}$ не совпадают.
Помимо магнитной восприимчивости в магнетиках используют другую безразмерную физическую величину, которая характеризует магнитные свойства вещества -- это относительная магнитная проницаемость (или просто магнитная проницаемость ($\mu $)) вещества. Причем:
\[\mu =1+\varkappa \ \left(11\right).\]Тогда между индукцией магнитного поля в магнетике и напряженностью магнитного поля существует следующая связь:
\[\overrightarrow{B}=\mu {\mu }_0\overrightarrow{H}\left(12\right).\]Формула (12) показывает, что в изотропных средах векторы $\overrightarrow{B}$ и $\overrightarrow{H}$ имею одинаковое направление, однако по модулю напряженность поля в $\mu {\mu }_0$ раз меньше.
Задание: По оси бесконечного прямого круглого цилиндра радиуса R течет ток силы I. Магнитная проницаемость вещества цилиндра равна $\mu $. Вне цилиндра вакуум (${\mu }_v=1$). Найдите формулу для вычисления напряженности во всех точках пространства.
Решение:
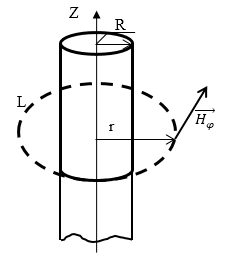
Рис. 1
Пусть ток течет в направлении оси Z. Линиями напряженности такого цилиндра являются концентрические окружности с центрами, которые лежат на оси цилиндра.
В качестве контура интегрирования (L) возьмем окружность радиусом r, центр окружности лежит на оси цилиндра, плоскость окружности перпендикулярна току. По закону полного тока для напряженности магнитного поля имеем:
\[\oint\limits_L{\overrightarrow{H\ }\overrightarrow{dl}}=H_{\varphi }2\pi r=I\left(1.1\right).\]Из (1.1) выразим напряженность поле, получим:
\[H_{\varphi }=\frac{I}{2\pi r}\left(1.2\right),\]где $H_{\varphi }$ -- напряжённость магнитного поля, касательная к окружности. В таком случае индукция магнитного поля равна:
\[B_{\varphi }=\left\{ \begin{array}{c} \mu {\mu }_0H_{\varphi }=\mu {\mu }_0\frac{I}{2\pi r}\ (при\ 0\le r\le R) \\ {\mu }_0H_{\varphi }={\mu }_0\frac{I}{2\pi r}\left(при\ r\ge R\right). \end{array} \right.\]На границе цилиндра индукция магнитного поля терпит разрыв.
Ответ: $B_{\varphi }=\left\{ \begin{array}{c} \mu {\mu }_0H_{\varphi }=\mu {\mu }_0\frac{I}{2\pi r}\ (при\ 0\le r\le R) \\ {\mu }_0H_{\varphi }={\mu }_0\frac{I}{2\pi r}\left(при\ r\ge R\right). \end{array} \right.$.Задание: Найдите намагниченность меди и магнитную индукцию поля, если удельная магнитная восприимчивость вещества ${\varkappa }_u=-1,1\cdot {10}^{-9}\frac{м^3}{кг}.$ Напряженность магнитного поля равна ${10}^6\frac{А}{м}$.
Решение:
Магнитная восприимчивость ($\varkappa $) связана с удельной магнитной восприимчивостью (${\varkappa }_u$) соотношением:
\[\varkappa =\rho {\varkappa }_u\left(2.1\right),\]где $\rho =8930\frac{кг}{м^3}$ -- массовая плотность меди.
Намагниченность имеет связь с напряженностью магнитного поля, которая имеет вид (считаем медь изотропной):
\[J=\varkappa H=\rho {\varkappa }_uH\ \left(2.2\right).\]Индукция магнитного поля, также связана с напряженностью:
\[B=\mu {\mu }_0H={\mu }_0(H+J)\left(2.3\right).\]Так как все величины даны в СИ, проведем вычисления:
\[J=8930\cdot \left(-1,1\cdot {10}^{-9}\right){10}^6=-9,823\left(\frac{А}{м}\right).\] \[B=4\pi \cdot {10}^{-7}\left(9,823+{10}^6\right)=1,26\ \left(Тл\right).\]Ответ: $J=-9,823\frac{А}{м},\ B=1,26\ Тл.$











